Section B.2 Entering Expressions
¶Subsection Parentheses
Order of Operations: The calculator follows the standard order of operations.
Example B.6.
Compute \(2+3\cdot 4\text{.}\) Press
\(2\,\) + \(\,3\,\) X \(\,4\) ENTER
Ans. \(14\)
Example B.7.
Compute \((2+3)\cdot4\text{.}\) Press
( \(\,2\,\) + \(\,3\,\) ) X \(\,4\) ENTER
Ans. \(20\)
Example B.8.
Compute \(\dfrac{1}{2\cdot 3} \text{.}\) Press
\(1 \,\boxed{\div} \) ( \(\,2\,\) X \(\,3\,\) ) ENTER
Ans. \(0.1666666667\)
Example B.9.
Compute \(\dfrac{1+3}{2} \text{.}\) Press
( \(1 \, \) + \(\,3\,\) ) \(\boxed{ \div } \,2\,\) ENTER
Ans. \(2\)
Subsection Exponents and Powers
Exponents: We use the caret key, ^ , to enter exponents or powers.
Example B.10.
Evaluate \(2^{10}\text{.}\)
\(2\) ^ \(10\) ENTER
Ans. \(1024\)
Squaring: There is a short-cut key for squaring, \(\boxed{x^2}\text{.}\)
Example B.11.
Evaluate \(57^{2}\text{.}\)
\(57~\boxed{x^2}\,\) ENTER
Ans. \(3249\)
Fractional Exponents: Fractional exponents must be enclosed in parentheses!
Example B.12.
Evaluate \(8^{2/3}\text{.}\)
\(8\,\) ^ ( \(2 ~ \boxed{\div} \, 3 \,\) ) ENTER
Ans. \(4\)
Subsection Roots
Square Roots: We access the square root by pressing 2nd \(\boxed{x^2} \text{,}\) and the display shows \(\sqrt{}(\text{.}\) The calculator automatically gives an open parenthesis for the square root, but not a close parenthesis.
Example B.13.
Evaluate \(\sqrt{2} \text{.}\)
2nd \(\boxed{x^2} \,2\,\) ) ENTER
Ans. \(1.414213562\)
Example B.14.
Evaluate \(\sqrt{9+16} \text{.}\)
2nd \(\boxed{x^2} \,9+16\,\) ) ENTER
Ans. \(5\)
In the next example, note that we must enter ) at the end of the radicand to tell the calculator where the radical ends.
Example B.15.
Evaluate \(\sqrt{9}+16 \text{.}\)
2nd \(\boxed{x^2} \,9\) ) \({}+{}16\,\) ENTER
Ans. \(19\)
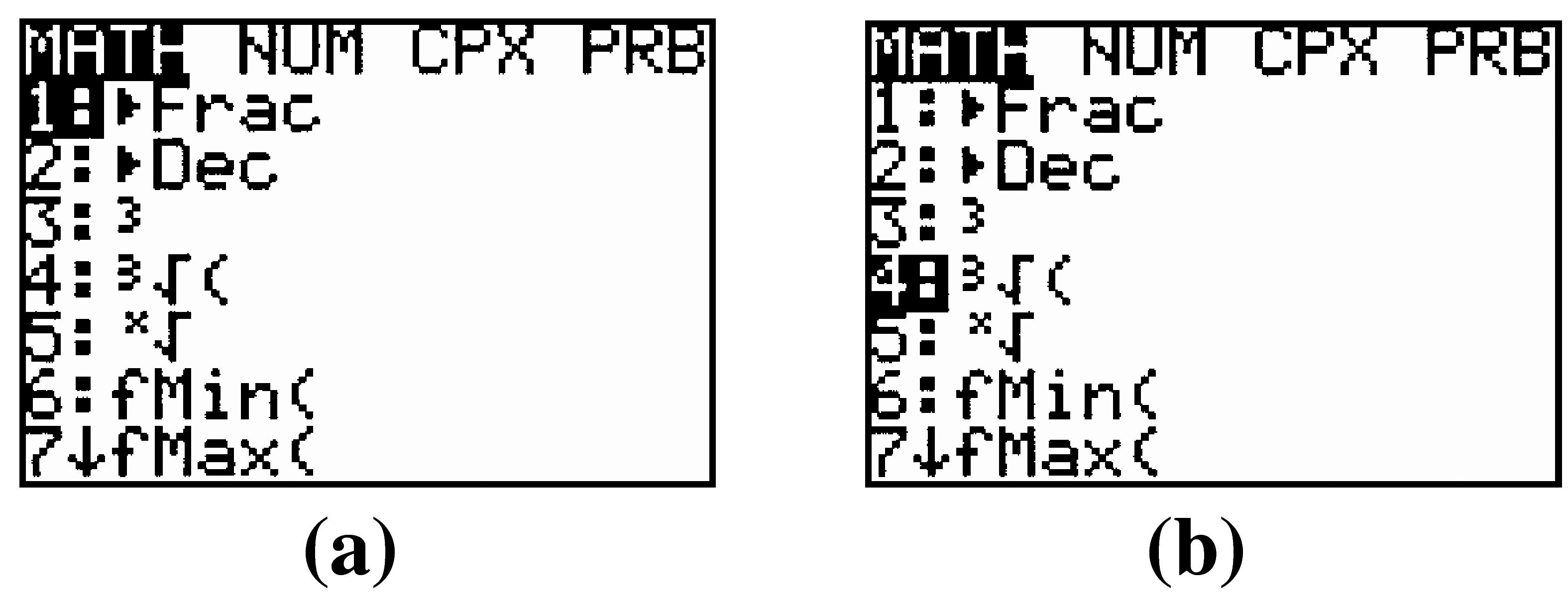
Cube Roots: For cube roots, we press MATH to open the Math menu and press \(4\) (see Figure B.16).
Example B.17.
Compute \(\sqrt[3]{1728} \text{.}\)
MATH \(~4~\) \(\, 1728\,\) ) ENTER
Ans. \(12\)
For evaluating cube roots and square roots, ) can be omitted if there are no operations following the radical.
Other Roots: For \(n\)th roots, we press MATH to open the Math menu and press \(5\) (see Figure B.16a). The calculator symbol for \(n\)th roots, \(\sqrt[x]{~} \text{,}\) does not include an open parenthesis,(. If the radicand includes an operation, we must enclose it in parentheses.
Example B.18.
Compute \(\sqrt[10]{2\cdot 512} \text{.}\)
\(10\,\)MATH \(~5~\) ( \(2\) x \(512\) ) ENTER
Ans. \(2\)
Notice that we enter the index 10 before the radical symbol.
Subsection Absolute Value
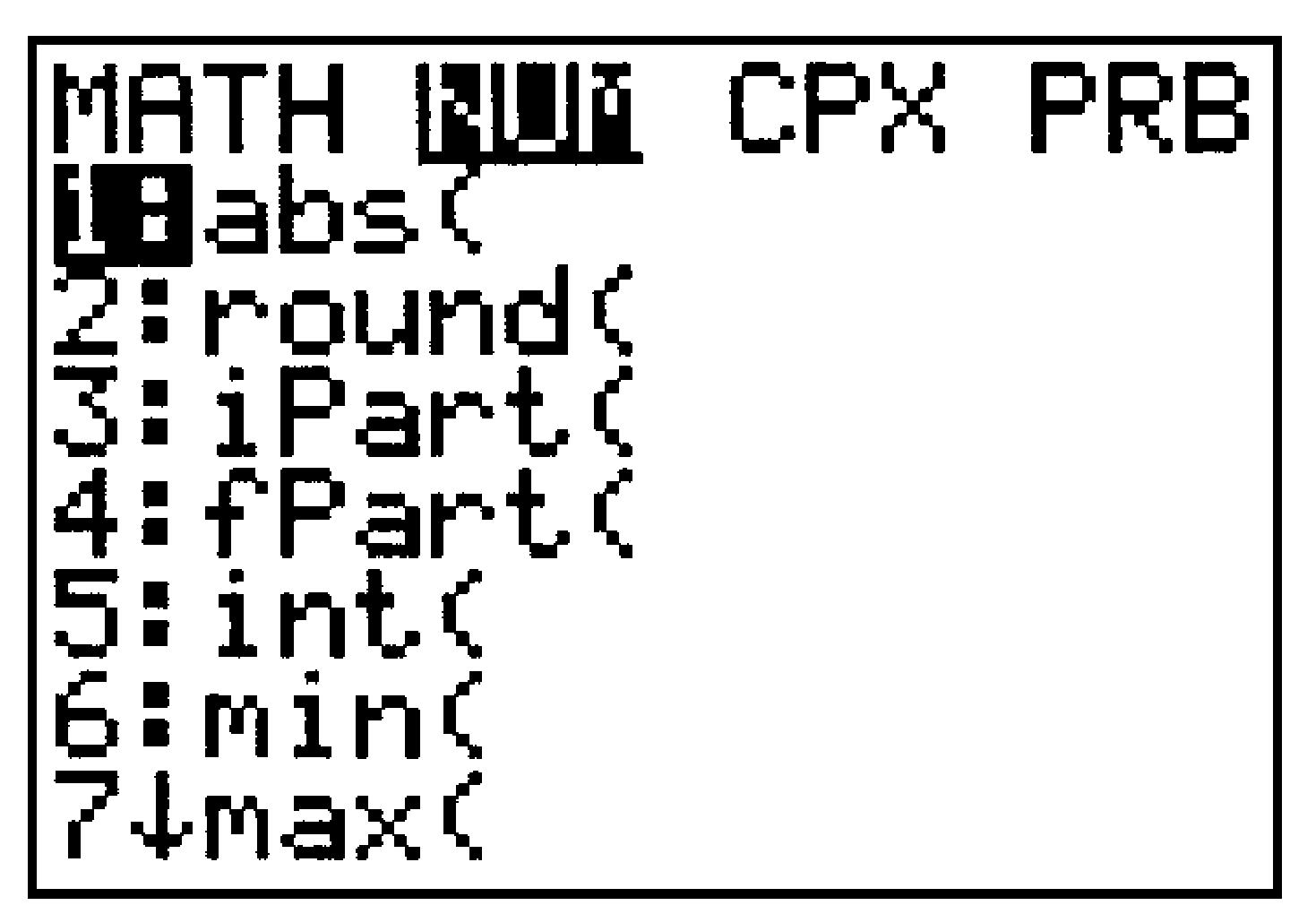
TI calculators use \(abs (x)\) instead of \(\abs{x}\) to denote the absolute value of \(x\text{.}\) The absolute value function is the first entry in the MATH NUM menu (see Figure B.19). The calculator gives ( for the absolute value function, but not ).
Example B.20.
Evaluate \(\dfrac{\abs{21\cdot 54 - 81}}{-9} \text{.}\)
MATH \(\boxed{\rightarrow}\) ENTER \(21\) X \(54\) - \(81\) ) \(\,\boxed{\div} \) (-) \(9\) ENTER
Ans. \(-117\)
Subsection Scientific Notation
The TI calculators display numbers in scientific notation when the numbers use too many digits to display.
Example B.21.
Compute \(123,456,789^2 \text{.}\) Enter
\(123456789 ~ \boxed{x^2}\) ENTER
Ans. \(1.524157875 \text{ E }16\)
This is how the calculator displays the number \(1.524157875 \times 10^{16}\text{.}\) Notice that the power \(10^{16}\) is displayed as \(\text{ E }16\text{.}\)
To enter a number in scientific form, we use the key labeled EE, or 2nd ,.
Example B.22.
To enter \(3.26 \times 10^{18}\text{,}\) use the keying sequence
\(3.26\) 2nd , (-) \(18\) ENTER
Ans. \(3.26 \text{ E}\) \(-18\)
Troubleshooting.
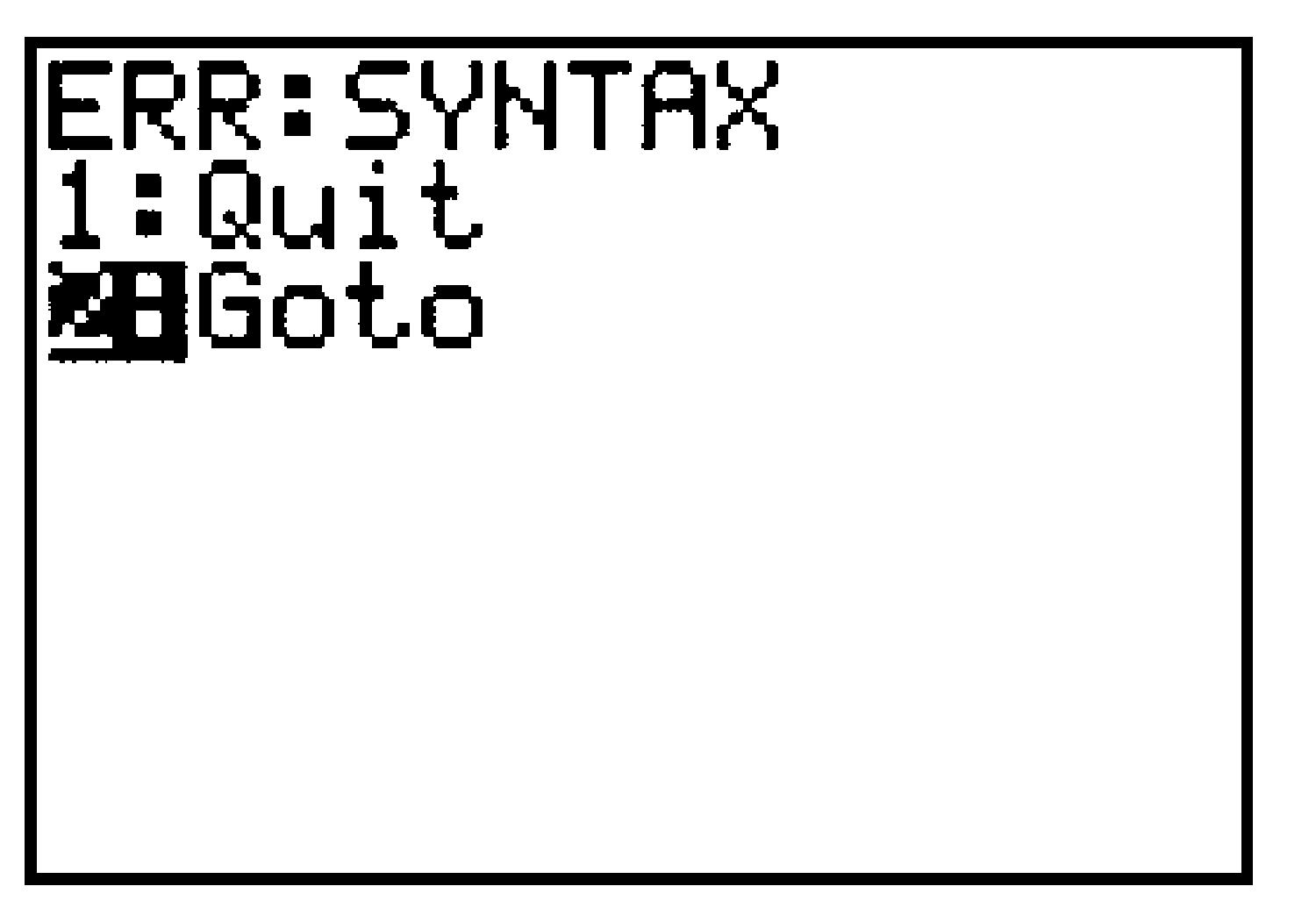
If your calculator gives you an error message like this, you may have made one of the following common mistakes:
Using the negative key,
(-), when you wanted the subtraction key,-, or vice versa.Omitting a
(or). Each(should have a matching).
Press \(2\) to Go to the error, and see Editing Expressions B.3 below.
