Skip to main content

Section A.7 Polynomials and Factoring

In Section A.6, we used the first law of exponents to multiply two or more monomials. In this section, we review techniques for multiplying and factoring polynomials of several terms.

Subsection Polynomials

A polynomial is a sum of terms in which all the exponents on the variables are whole numbers and no variables appear in the denominator or under a radical. The expressions

\begin{equation*} 0.1 R^4, ~~d^2 + 32 d - 21, ~~\text{ and }~~128x^3 - 960x^2 + 8000 \end{equation*}

are all examples of polynomials in one variable.

An algebraic expression consisting of one term of the form \(cx^n\text{,}\) where \(c\) is a constant and \(n\) is a whole number, is called a monomial. For example,

\begin{equation*} y3, ~~-3x^8, ~~\text{ and } ~~0.1R^4 \end{equation*}

are monomials. A polynomial is just a sum of one or more monomials.

A polynomial with exactly two terms, such as \(\dfrac{1}{2}n^2 + \dfrac{1}{2}n\text{,}\) is called a binomial. A polynomial with exactly three terms, such as \(d^2 + 32 d - 21\) or \(128x^3 - 960x^2 + 8000\text{,}\) is called a trinomial. We have no special names for polynomials with more than three terms.

Which of the following expressions are polynomials?

  1. \(\pi r^2\)

  2. \(23.4s^6 - 47.9s^4\)

  3. \(\dfrac{2}{3}w^3 - \dfrac{7}{3}w^2 + \dfrac{1}{3}w\)

  4. \(7 + m^{-2}\)

  5. \(\dfrac{x-2}{x+2}\)

  6. \(\sqrt[3]{4y}\)

Solution

The first three are all polynomials. In fact, (a) is a monomial, (b) is a binomial, and (c) is a trinomial. The last three are not polynomials. The variable in (d) has a negative exponent, the variable in (e) occurs in the denominator, and the variable in (f) occurs under a radical.

In a polynomial containing only one variable, the greatest exponent that appears on the variable is called the degree of the polynomial. If there is no variable at all, then the polynomial is called a constant, and the degree of a constant is zero.

Give the degree of each polynomial.

  1. \(b^3 - 3b^2 + 3b - 1\)

  2. \(10^{10}\)

  3. \(-4w^3\)

  4. \(s^2 - s^6\)

Solution

  1. This is a polynomial in the variable \(b\text{,}\) and because the greatest exponent on \(b\) is \(3\text{,}\) the degree of this polynomial is \(3\text{.}\)

  2. This is a constant polynomial, so its degree is \(0\text{.}\) (The exponent on a constant does not affect the degree.)

  3. This monomial has degree \(3\text{.}\)

  4. This is a binomial of degree \(6\text{.}\)

We can evaluate a polynomial just as we evaluate any other algebraic expression: We replace the variable with a number and simplify the result.

Let \(p(x) = -2x^2 + 3x - 1\text{.}\) Evaluate each of the following.

  1. \(p(2)\)

  2. \(p(-1)\)

  3. \(p(t)\)

  4. \(p(t+3)\)

Solution

In each case, we replace \(x\) by the given value.

  1. \(p(\alert{2})=-2(\alert{2})^2 + 3(\alert{2}) - 1=-8+6-1=-3\)

  2. \(p(\alert{-1})=-2(\alert{-1})^2 + 3(\alert{-1}) - 1=-2+(-3)-1=-6\)

  3. \(p(\alert{t})=-2(\alert{t})^2 + 3(\alert{t}) - 1=--2t^2+3t-1\)

  4. \(\begin{aligned}[t] \amp \\ p(\alert{t+3})\amp =-2(\alert{t+3})^2 + 3(\alert{t+3}) - 1\\ \amp = -2(t^2+6t+9)+3(t+3)-1\\ \amp = -2t^2-9t-10 \end{aligned}\)

Subsection Products of Polynomials

To multiply polynomials, we use a generalized form of the distributive property:

\begin{equation*} a(b + c + d + \cdots) = ab + ac + ad + \cdots \end{equation*}

To multiply a polynomial by a monomial, we multiply each term of the polynomial by the monomial.

  1. \(\begin{aligned}[t] \amp\\ 3x(x + y + z) \amp = 3x(x) + 3x(y) + 3x(z)\\ \amp = 3x^2+3xy+3xz \end{aligned}\)

  2. \(\begin{aligned}[t] \amp\\ -2ab^2(3a^2 - ab + 2b^2) \amp = -2ab^2(3a^2) - 2ab^2(-ab) - 2ab^2(2b^2)\\ \amp = -6a^3b^2+2a^2b^3-4ab^4 \end{aligned}\)

Subsection Products of Binomials

Products of binomials occur so frequently that it is worthwhile to learn a shortcut for this type of multiplication. We can use the following scheme to perform the multiplication mentally. (See Figure A.51.)

figure identifying thefirst, outer, inner, and last terms in a binomial product
Figure A.51.

This process is sometimes called the FOIL method, where FOIL represents

\begin{align*} \amp\text{the product of the} \blert{~F}\text{irst terms}\\ \amp\text{the product of the} \blert{~O}\text{uter terms}\\ \amp\text{the product of the} \blert{~I}\text{nner terms}\\ \amp\text{the product of the} \blert{~L}\text{ast terms} \end{align*}
\begin{align*} (2x - 1)(x + 3) \amp = 2x^2 + 6x - x - 3\\ \amp = 2x^2 + 5x - 3 \end{align*}

Subsection Factoring

We sometimes find it useful to write a polynomial as a single term composed of two or more factors. This process is the reverse of multiplication and is called factoring. For example, observe that

\begin{equation*} 3x^2 + 6x = 3x(x + 2) \end{equation*}

We will only consider factorization in which the factors have integer coefficients.

Subsection Common Factors

We can factor a common factor from a polynomial by using the distributive property in the form

\begin{equation*} ab + ac = a(b + c) \end{equation*}

We first identify the common factor. For example, each term of the polynomial

\begin{equation*} 6x^3 + 9x^2 - 3x \end{equation*}

contains the monomial \(3x\) as a factor; therefore,

\begin{equation*} 6x^3 + 9x^2 - 3x = 3x (\underline{\hspace{6.818181818181818em}}) \end{equation*}

Next, we insert the proper polynomial factor within the parentheses. This factor can be determined by inspection. We ask ourselves for monomials that, when multiplied by \(3x\text{,}\) yield \(6x^3\text{,}\) \(9x^2\text{,}\) and \(-3x\text{,}\) respectively, and obtain

\begin{equation*} 6x^3 + 9x^2 - 3x = 3x(2x^2 + 3x - 1) \end{equation*}

We can check the result of factoring an expression by multiplying the factors. In the example above,

\begin{equation*} 3x(2x^2 + 3x - 1) = 6x^3 + 9x^2 - 3x \end{equation*}

  1. \(\begin{aligned}[t] \\ 18x^2 y - 24xy^2 \amp = 6xy(\text{?} - \text{?}) \\ \amp = 6xy(3x - 4y) \end{aligned}\)

    because

    \begin{equation*} 6xy(3x - 4y) = 18x^2 y - 24xy^2 \end{equation*}

  2. \(\begin{aligned}[t] \\ y(x - 2) + z(x - 2) \amp = (x - 2)(\text{?} - \text{?}) \\ \amp = (x - 2)(y + z) \end{aligned}\)

    because

    \begin{equation*} (x - 2)(y + z) = y(x - 2) + z(x - 2) \end{equation*}

Subsection Opposite of a Binomial

It is often useful to factor \(-1\) from the terms of a binomial.

\begin{align*} a - b \amp = (-1)(-a + b)\\ \amp = (-1)(b - a) = -(b - a) \end{align*}

Hence, we have the following important relationship.

Opposite of a Binomial.
\begin{equation*} a-b=-(b-a) \end{equation*}

That is, \(a-b\) and \(b-a\) are opposites or negatives of each other.

  1. \(3x - y = -(y - 3x)\)

  2. \(a - 2b = -(2b - a)\)

Subsection Polynomial Division

We can divide one polynomial by a polynomial of lesser degree. The quotient will be the sum of a polynomial and a simpler algebraic fraction.

If the divisor is a monomial, we can simply divide the monomial into each term of the numerator.

Divide \(\dfrac{9x^3 - 6x^2 + 4}{3x}\)

Solution

Divide \(3x\) into each term of the numerator.

\begin{align*} \frac{9x^3 - 6x^2 + 4}{3x} \amp = \frac{9x^3}{3x}- \frac{6x^2}{3x}+ \frac{4}{3x}\\ \amp = 3x^2 - 2x + \frac{4}{3x} \end{align*}

The quotient is the sum of a polynomial, \(3x^2 - 2x\text{,}\) and an algebraic fraction, \(\dfrac{4}{3x}\text{.}\)

If the denominator is not a monomial, we can use a method similar to the long division algorithm used in arithmetic.

Divide \(\dfrac{2x^2+x-7}{x+3}\)

Solution

First write

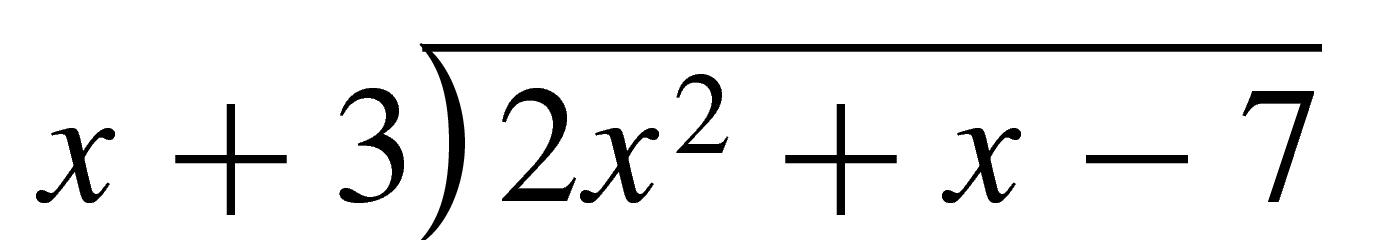
long division box

and divide \(2x^2\) (the first term of the numerator) by \(x\) (the first term of the denominator) to obtain \(2x\text{.}\) (It may be helpful to write down the division: \(\dfrac{2x^2}{2x}=x\text{.}\)) Write \(2x\) above the quotient bar as the first term of the quotient, as shown below.

Next, multiply \(x+3\) by \(2x\) to obtain \(2x^2 + 6x\text{,}\) and subtract this product from \(2x^2 + x - 7\text{:}\)

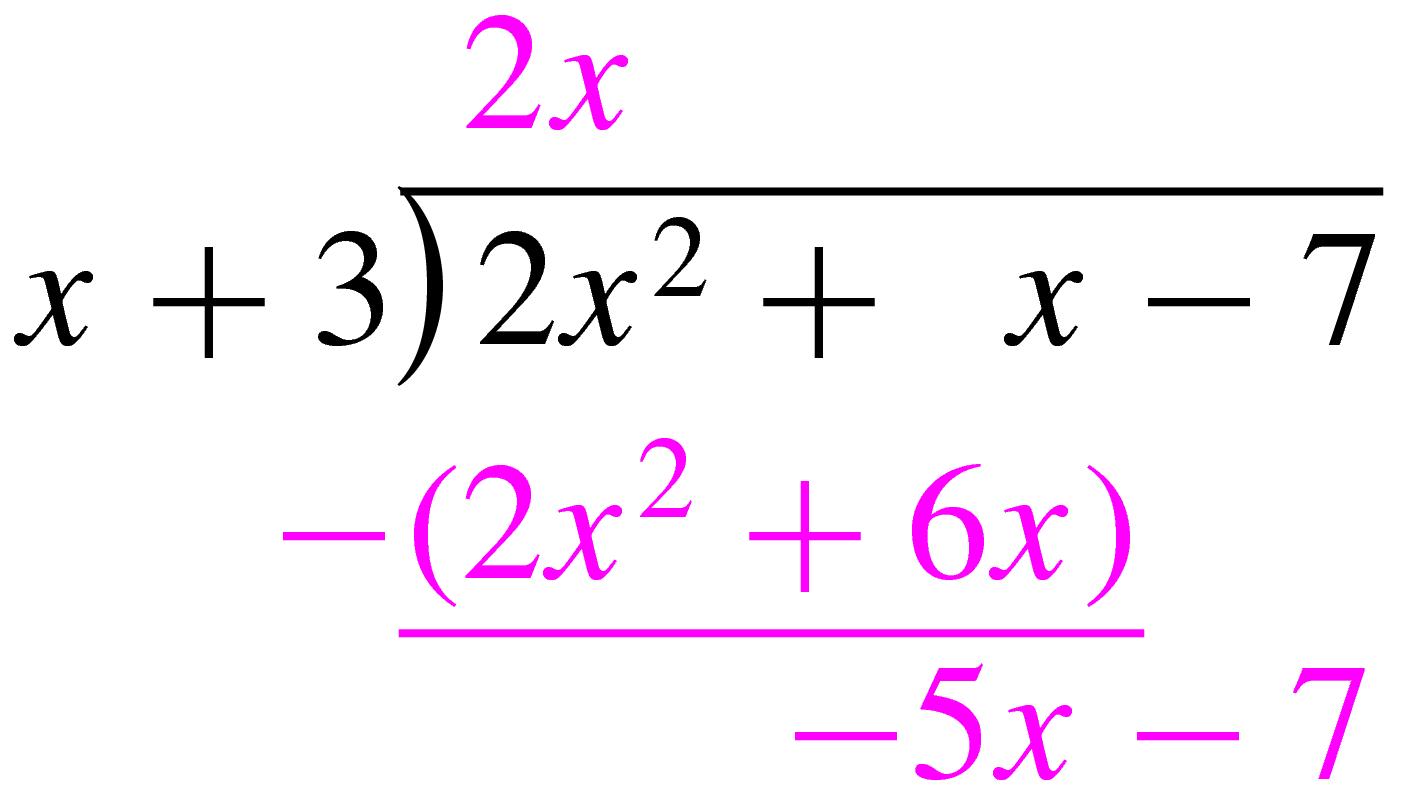
long division box

Repeating the process, divide \(-5x\) by \(x\) to obtain \(-5\text{.}\) Write \(-5\) as the second term of the quotient. Then multiply \(x+3\) by \(-5\) to obtain \(-5x - 15\text{,}\) and subtract:

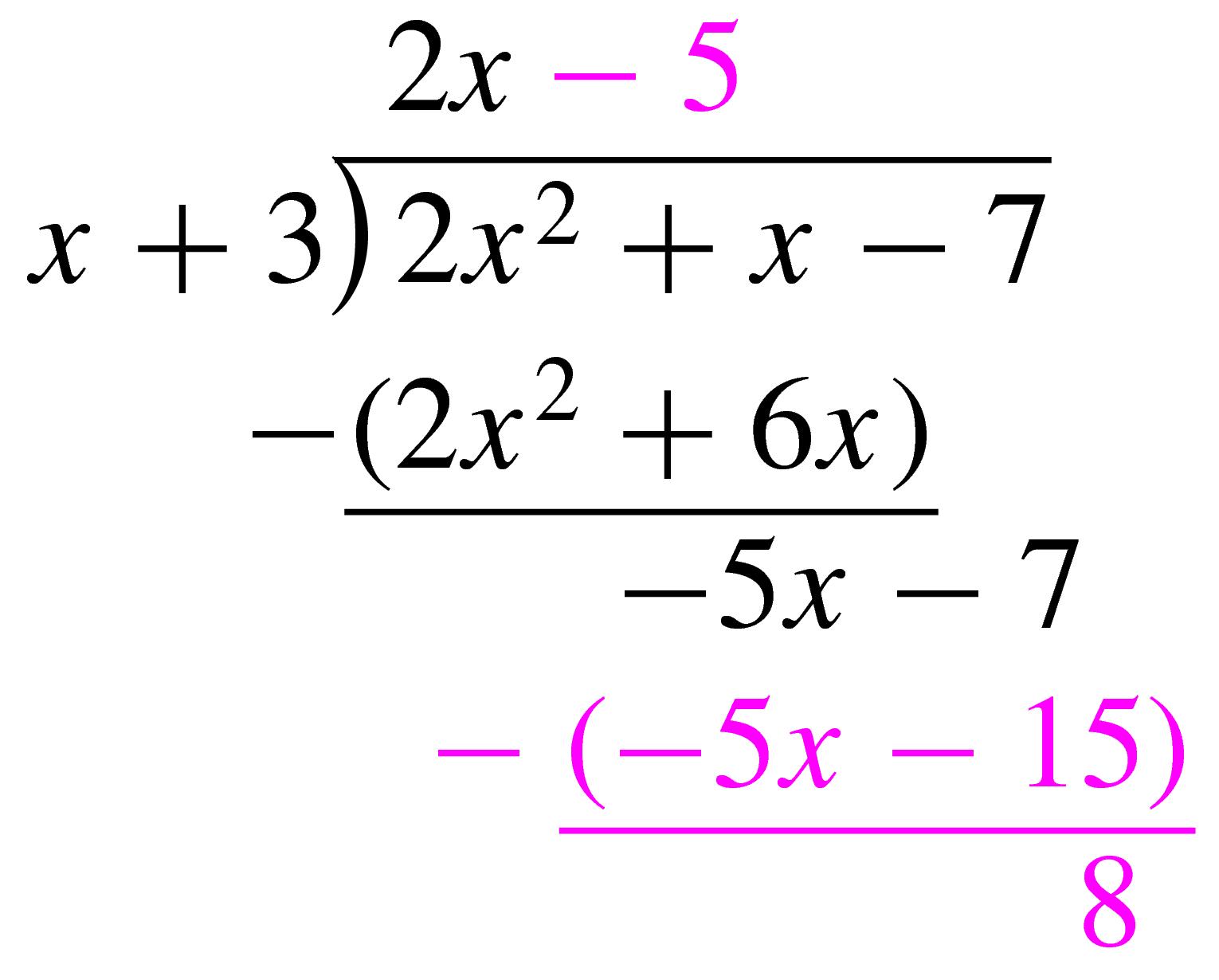
long division box

Because the degree of \(8\) is less than the degree of \(x + 3\text{,}\) the division is finished. The quotient is \(2x - 5\text{,}\) with a remainder of \(8\text{.}\) We write the remainder as a fraction to obtain

\begin{equation*} \frac{2x^2 + x - 7}{x + 3}= 2x - 5 + \frac{8}{x + 3} \end{equation*}

When using polynomial division, it helps to write the polynomials in descending powers of the variable. If the numerator is missing any terms, we can insert terms with zero coefficients so that like powers will be aligned. For example, to perform the division

\begin{equation*} \frac{3x - 1 + 4x^3}{2x-1} \end{equation*}

we first write the numerator in descending powers as \(4x^3 + 3x - 1\text{.}\) We then insert \(0x^2\) between \(4x^3\) and \(3x\) and set up the quotient as

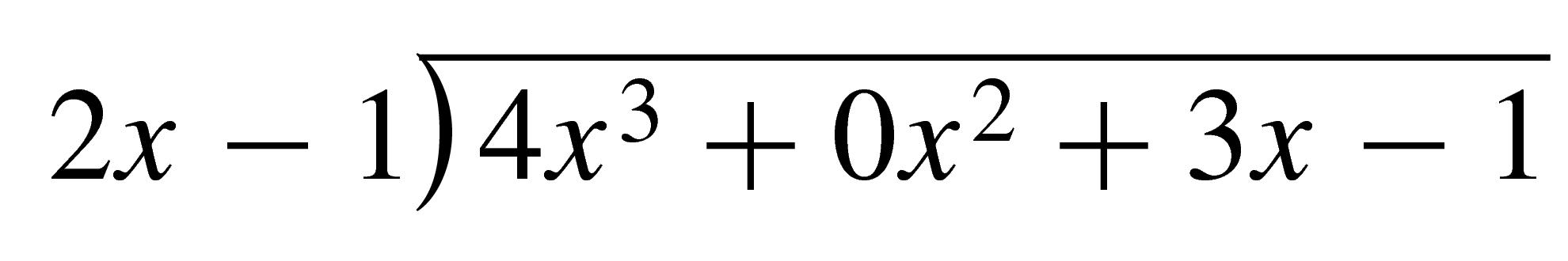
long division box

We then proceed as in Example A.56. You can check that the quotient is

\begin{equation*} 2x^2 + x + 2 + \frac{1}{2x-1} \end{equation*}

Subsection Section Summary

Subsubsection Vocabulary

Look up the definitions of new terms in the Glossary.

  • Polynomial

  • Common factor

  • Degree

  • Constant

  • Trinomial

  • Monomial

  • Binomial

Subsubsection SKILLS

Practice each skill in the exercises listed.

  1. Identify polynomials: #1–12

  2. Evaluate polynomials: #13–20

  3. Multiply polynomials: #21–42

  4. Factor out a common factor: #43–68

  5. Divide polynomials: #69–80

Exercises Exercises A.7

For Problems 1-8, identify the polynomial as a monomial, a binomial, or a trinomial. Give the degree of the polynomial.

1.

\(2x^3-x^2 \)

2.

\(x^2-2x+1\)

3.

\(5n^4\)

4.

\(3n+1\)

5.

\(3r^2-4r+2\)

6.

\(r^3\)

7.

\(y^3-2y^2-y\)

8.

\(3y^2+1\)

Which of the expressions in Problems 9-12 are not polynomials?

9.

  1. \(1-0.04t^2\)

  2. \(3x^2-4x+\dfrac{2}{x}\)

  3. \(2\sqrt{z}-7z^3+2 \)

  4. \(\sqrt{2}w^3+\dfrac{3}{4}w^2-w \)

10.

  1. \(\sqrt{3}p^2-7p+2 \)

  2. \(2h^{4/3}+6h^{1/3}-2 \)

  3. \(\dfrac{2}{x^2-6x+5} \)

  4. \(\dfrac{1}{4}y^{-2}+3y^{-1}+4 \)

11.

  1. \(\dfrac{1}{m^2+3} \)

  2. \(v^2-16+2^v \)

  3. \(\sqrt{x^3-4x} \)

  4. \(\dfrac{m^4}{12} \)

12.

  1. \(3^t-5t^3+2 \)

  2. \(\dfrac{q+3}{q-1} \)

  3. \(c^{1/2}-c \)

  4. \(\sqrt[3]{d+1} \)

For Problems 13-20, evaluate the polynomial function for the given values of the variable.

13.

\(P(x)=x^3-3x^2+x+1 \)

  1. \(x=2\)

  2. \(x=-2\)

  3. \(x=2b\)

14.

\(P(x)=2x^3+x^2-3x+4 \)

  1. \(x=3\)

  2. \(x=-3\)

  3. \(x=-a\)

15.

\(Q(t)=t^2+3t+1 \)

  1. \(t=\dfrac{1}{2} \)

  2. \(t=-\dfrac{1}{3} \)

  3. \(t=-w \)

16.

\(Q(t)=2t^2-t+1 \)

  1. \(t=\dfrac{1}{4} \)

  2. \(t=-\dfrac{1}{2} \)

  3. \(t=3v \)

17.

\(R(z)=3z^4-2z^2+3 \)

  1. \(z=1.8 \)

  2. \(z=-2.6 \)

  3. \(z=k-1 \)

18.

\(R(z)=z^4+4z-2 \)

  1. \(z=2.1 \)

  2. \(z=-3.1 \)

  3. \(z=h+2 \)

19.

\(N(a)=a^6-a^5 \)

  1. \(a=-1 \)

  2. \(a=-2 \)

  3. \(a=\dfrac{m}{3} \)

20.

\(N(a)=a^5-a^4 \)

  1. \(a=-1 \)

  2. \(a=-2 \)

  3. \(a=\dfrac{q}{2} \)

For Problems 21-42, write the product as a polynomial and simplify.

21.

\(4y(x-2y) \)

22.

\(3x(2x+y) \)

23.

\(-6x(2x^2-x+1) \)

24.

\(-2y(y^2-3y+2) \)

25.

\(a^2b(3a^2-2ab-b) \)

26.

\(ab^3(-a^2 b^2+4ab-3) \)

27.

\(2x^2y^2(4xy^4-2xy-3x^3y^2) \)

28.

\(5x^2y^2(3x^4y^2+3x^2y-xy^6) \)

29.

\((n+2)(n+8) \)

30.

\((r-1)(r-6) \)

31.

\((r+5)(r-2) \)

32.

\((z-3)(z+5) \)

33.

\((2z+1)(z-3) \)

34.

\((3t-1)(2t+1) \)

35.

\((4r+3s)(2r-s) \)

36.

\((2z-w)(3z+5w) \)

37.

\((2x-3y)(3x-2y) \)

38.

\((3a+5b)(3a+4b) \)

39.

\((3t-4s)(3t+4s) \)

40.

\((2x-3z)(2x+3z) \)

41.

\((2a^2+b^2)(a^2-3b^2) \)

42.

\((s^2-5t^2)(3s^2+2t^2) \)

For Problems 43-60, factor completely. Check your answers by multiplying factors.

43.

\(4x^2 z+8xz \)

44.

\(3x^2y+6xy \)

45.

\(3n^4-6n^3+12n^2 \)

46.

\(2x^4-4x^2+6x \)

47.

\(15r^2s+18rs^2-3r \)

48.

\(2x^2y^2-3xy+5x^2 \)

49.

\(3m^2n^4-6m^3n^3+14m^3n^2 \)

50.

\(6x^3y-6xy^3+12x^2y^2 \)

51.

\(15a^4b^3c^4-12a^2b^2c^5+6a^2b^3c^4 \)

52.

\(14xy^4z^3+21x^2y^3z^2-28x^3y^2z^5 \)

53.

\(a(a+3)+b(a+3) \)

54.

\(b(a-2)+a(a-2) \)

55.

\(y(y-2)-3x(y-2) \)

56.

\(2x(x+3)-y(x+3) \)

57.

\(4(x-2)^2-8x(x-2)^3 \)

58.

\(6(x+1)-3x(x+1)^2 \)

59.

\(x(x-5)^2-x^2(x-5)^3 \)

60.

\(x^2(x+3)^3-x(x+3)^2 \)

For Problems 61-68, supply the missing factors or terms.

61.

\(3m-n=-(~~~\text{ ? }~~~) \)

62.

\(2a-b=-(~~~\text{ ? }~~~) \)

63.

\(-2x+2=-2(~~~\text{ ? }~~~) \)

64.

\(-6x-9=-3(~~~\text{ ? }~~~) \)

65.

\(-ab-ac=\text{ ? }(b+c) \)

66.

\(-a^2+ab=\text{ ? }(a-b) \)

67.

\(2x-y+3z=-(~~~\text{ ? }~~~) \)

68.

\(3x+3y-2z=-(~~~\text{ ? }~~~) \)

For Problems 69-80, divide.

69.

\(\dfrac{18r^2s^2-15rs+6}{3rs}\)

70.

\(\dfrac{8a^2x^2-4ax^2+ax}{2ax}\)

71.

\(\dfrac{15s^{10}-21s^5+6}{-3s^2}\)

72.

\(\dfrac{25m^6-15m^4+7}{-5m^3}\)

73.

\(\dfrac{4y^2+12y+7}{2y+1}\)

74.

\(\dfrac{4t^2-4t-5}{2t-1}\)

75.

\(\dfrac{x^3+2x^2+x+1}{x-2}\)

76.

\(\dfrac{2x^3-3x^2-2x+4}{x+1}\)

77.

\(\dfrac{4z^2+5z+8z^4+3}{2z+1}\)

78.

\(\dfrac{7-3t^3-23t^2+10t^4}{2t+3}\)

79.

\(\dfrac{x^4-1}{x-2}\)

80.

\(\dfrac{y^5+1}{y-1}\)