Skip to main content

Section B.7 Function Notation and Transformation of Graphs

Subsection Function Notation

The calculator uses \(Y_1 (X)\text{,}\) \(Y_2 (X)\text{,}\) and so on, instead of \(f (x)\text{,}\) \(g(x)\text{,}\) and so on, for function notation.

Evaluate \(f (x) = x^2 + 6x + 9\) for \(x = 3\text{.}\)

  1. Set \(Y_1 = X^2 + 6X + 9\text{,}\) and quit (2nd MODE) to the Home screen.

  2. To evaluate this function for \(X = 3\text{,}\) press

    VARS \(\boxed{\rightarrow}\) ENTER ENTER ( \(3\) ) ENTER

    See Figure B.43.

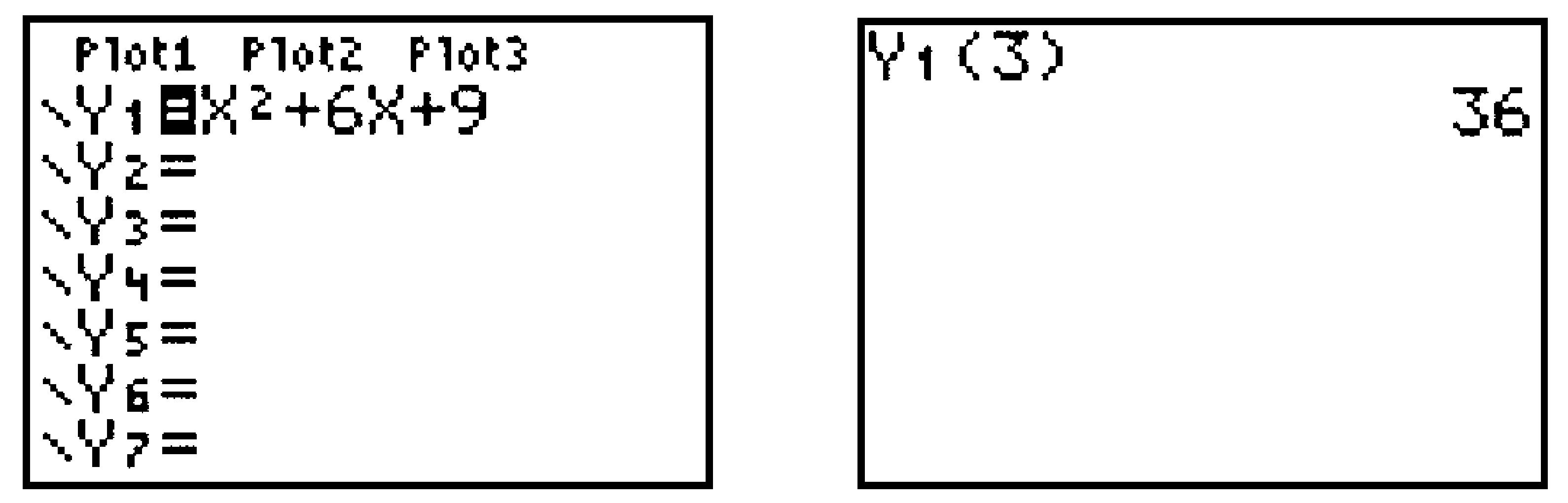
    GC evaluating a function
    Figure B.43.

Subsection Transformation of Graphs

We can use function notation to facilitate graphing transformations. In the examples below, we use \(f (x) = x^2\text{.}\)

Subsubsection Translations

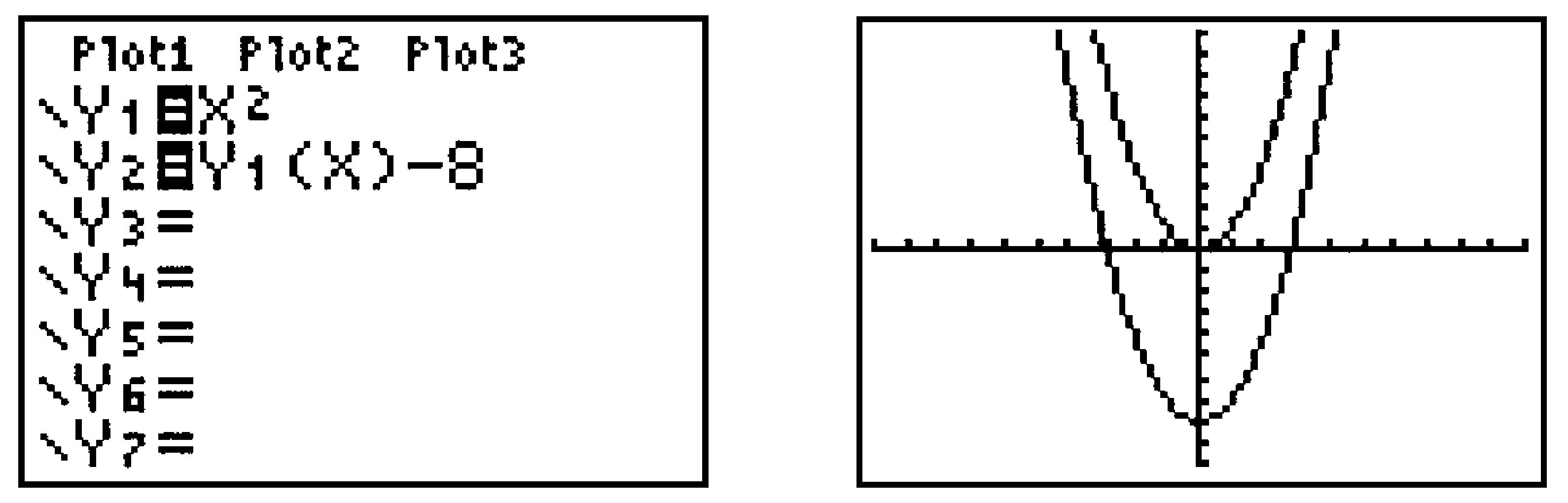
Compare the graphs of \(y = f (x) - 8\) and \(y = f (x - 8)\) with that of \(y = f (x)\text{.}\)

Define \(Y_1 = X^2\) and \(Y_2 =Y_1(X) - 8\) . Press ZOOM \(6\) to see the graphs (Figure B.45).

GC vertical shift of parabola
Figure B.45.

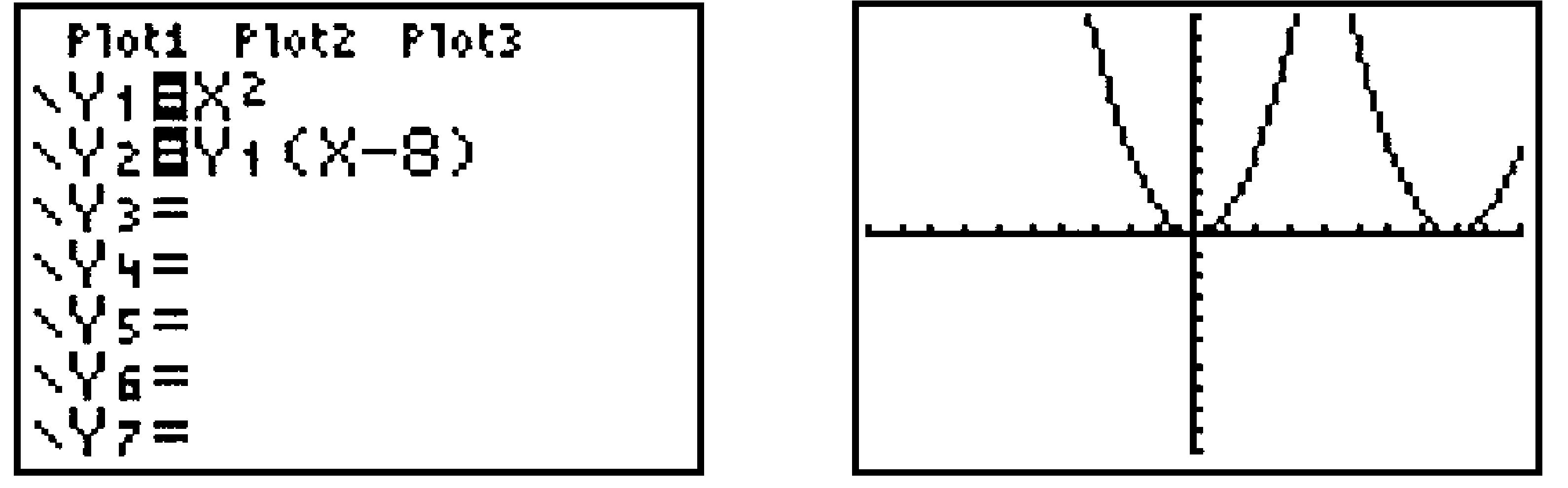
Define \(Y_1 = X^2\) and \(Y_2 =Y_1(X - 8)\text{.}\) Press ZOOM \(6\) to see the graphs (Figure B.46).

GC horizontal shift of parabola
Figure B.46.

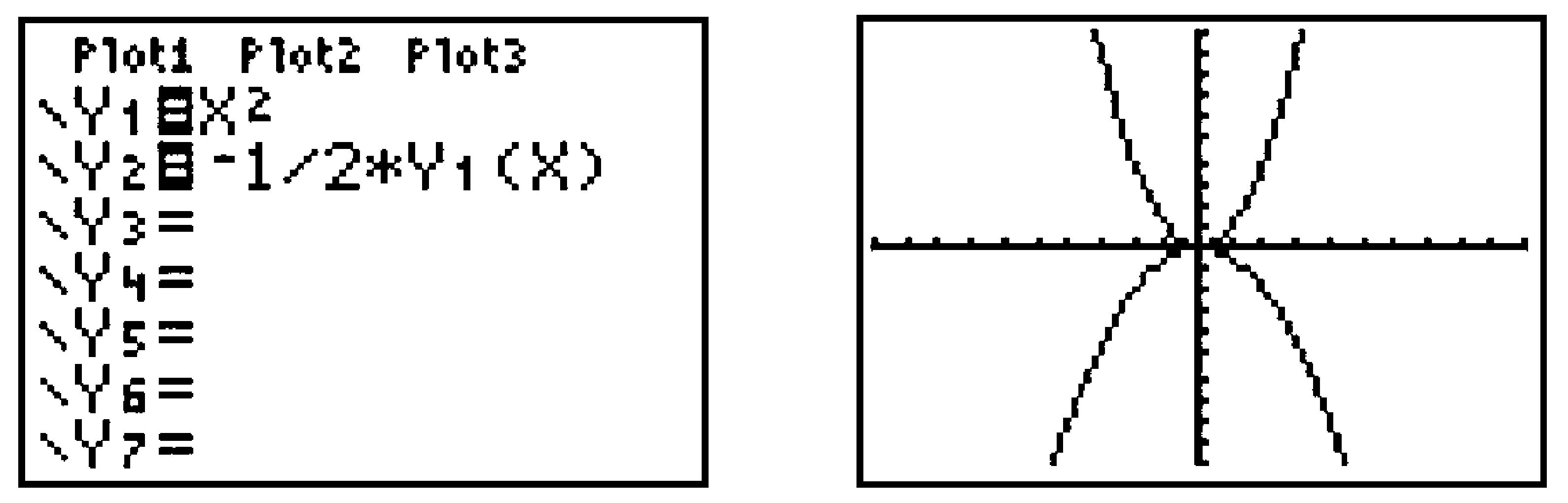
Subsubsection Vertical Scalings and Reflections

Compare the graph of \(y = \frac{-1}{2} f (x)\) with that of \(y = f (x)\text{.}\)

Define \(Y_1 = X^2\) and \(Y_2 = -1/2*Y_1(X)\text{.}\) Press to see the graphs (Figure B.47).

GC vertical reflection of parabola
Figure B.47.