Skip to main content

Section 1.2 Functions

Subsection Definition of Function

We often want to predict values of one variable from the values of a related variable. For example, when a physician prescribes a drug in a certain dosage, she needs to know how long the dose will remain in the bloodstream. A sales manager needs to know how the price of his product will affect its sales. A function is a special type of relationship between variables that allows us to make such predictions.

Suppose it costs $800 for flying lessons, plus $30 per hour to rent a plane. If we let \(C\) represent the total cost for \(t\) hours of flying lessons, then

\begin{equation*} C=800+30t ~~~~ (t\ge 0) \end{equation*}

Thus, for example

when \(t=\alert{0}\text{,}\) \(C=800+30(\alert{0})=800\)
when \(t=\alert{4}\text{,}\) \(C=800+30(\alert{4})=920\)
when \(t=\alert{10}\text{,}\) \(C=800+30(\alert{10})=1100\)

The variable \(t\) is called the input or independent variable, and \(C\) is the output or dependent variable, because its values are determined by the value of \(t\text{.}\) We can display the relationship between two variables by a table or by ordered pairs. The input variable is the first component of the ordered pair, and the output variable is the second component.

\(t\) \(C\) \((t,C)\)
\(0\) \(800\) \((0, 800)\)
\(4\) \(920\) \((4, 920)\)
\(10\) \(1100\) \((10,1100)\)

For this relationship, we can find the value of \(C\) for any given value of \(t\text{.}\) All we have to do is substitute the value of \(t\) into the equation and solve for \(C\text{.}\) Note that there can be only one value of \(C\) for each value of \(t\text{.}\)

Definition of Function.

A function is a relationship between two variables for which a unique value of the output variable can be determined from a value of the input variable.

Note 1.19.

What distinguishes functions from other variable relationships? The definition of a function calls for a unique value—that is, exactly one value of the output variable corresponding to each value of the input variable. This property makes functions useful in applications because they can often be used to make predictions.

  1. The distance, \(d\text{,}\) traveled by a car in 2 hours is a function of its speed, \(r\text{.}\) If we know the speed of the car, we can determine the distance it travels by the formula \(d = r \cdot 2\text{.}\)

  2. The cost of a fill-up with unleaded gasoline is a function of the number of gallons purchased. The gas pump represents the function by displaying the corresponding values of the input variable (number of gallons) and the output variable (cost).

  3. Score on the Scholastic Aptitude Test (SAT) is not a function of score on an IQ test, because two people with the same score on an IQ test may score differently on the SAT; that is, a person’s score on the SAT is not uniquely determined by his or her score on an IQ test.

  1. As part of a project to improve the success rate of freshmen, the counseling department studied the grades earned by a group of students in English and algebra. Do you think that a student’s grade in algebra is a function of his or her grade in English? Explain why or why not.

  2. Phatburger features a soda bar, where you can serve your own soft drinks in any size. Do you think that the number of calories in a serving of Zap Kola is a function of the number of fluid ounces? Explain why or why not.

Answer

  1. No, students with the same grade in English can have different grades in algebra.

  2. Yes, the number of calories is proportional to the number of fluid ounces.

A function can be described in several different ways. In the following examples, we consider functions defined by tables, by graphs, and by equations.

Subsection Functions Defined by Tables

When we use a table to describe a function, the first variable in the table (the left column of a vertical table or the top row of a horizontal table) is the input variable, and the second variable is the output. We say that the output variable is a function of the input.

  1. The table below shows data on sales compiled over several years by the accounting office for Eau Claire Auto Parts, a division of Major Motors. In this example, the year is the input variable, and total sales is the output. We say that total sales, \(S\text{,}\) is a function of \(t\text{.}\)

    Year \((t)\) Total sales \((S)\)
    2000 $612,000
    2001 $663,000
    2002 $692,000
    2003 $749,000
    2004 $904,000

  2. The table below gives the cost of sending printed material by first-class mail in 2016.

    Weight in ounces \((w)\) Postage \((P)\)
    \(0 \lt w \le 1 \) $0.47
    \(1 \lt w \le 2 \) $0.68
    \(2 \lt w \le 3 \) $0.89
    \(3 \lt w \le 4 \) $1.10
    \(4 \lt w \le 5 \) $1.31
    \(5 \lt w \le 6 \) $1.52
    \(6 \lt w \le 7 \) $1.73

    If we know the weight of the article being shipped, we can determine the required postage from the table. For instance, a catalog weighing 4.5 ounces would require $1.31 in postage. In this example, \(w\) is the input variable and \(p\) is the output variable. We say that \(p\) is a function of \(w\text{.}\)

  3. The table below records the age and cholesterol count for 20 patients tested in a hospital survey.

    Age Cholesterol count Age Cholesterol count
    53 217 \(\alert{51}\) \(\alert{209}\)
    48 232 53 241
    55 198 49 186
    56 238 \(\alert{51}\) \(\alert{216}\)
    \(\alert{51}\) \(\alert{227}\) 57 208
    52 264 52 248
    53 195 50 214
    47 203 56 271
    48 212 53 193
    50 234 48 172

    According to these data, cholesterol count is not a function of age, because several patients who are the same age have different cholesterol levels. For example, three different patients are 51 years old but have cholesterol counts of 227, 209, and 216, respectively. Thus, we cannot determine a unique value of the output variable (cholesterol count) from the value of the input variable (age). Other factors besides age must influence a person’s cholesterol count.

Decide whether each table describes \(y\) as a function of \(x\text{.}\) Explain your choice.

  1. \(x\) \(3.5\) \(2.0\) \(2.5\) \(3.5\) \(2.5\) \(4.0\) \(2.5\) \(3.0\)
    \(y\) \(2.5\) \(3.0\) \(2.5\) \(4.0\) \(3.5\) \(4.0\) \(2.0\) \(2.5\)
  2. \(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\)
    \(y\) \(17\) \(3\) \(0\) \(-1\) \(0\) \(3\) \(17\)
Answer

  1. No, for example, \(x = 3.5\) corresponds both to \(y = 2.5\) and also to \(y = 4.0\text{.}\)

  2. Yes, each value of \(x\) has exactly one value of \(y\) associated with it.

Subsection Functions Defined by Graphs

A graph may also be used to define one variable as a function of another. The input variable is displayed on the horizontal axis, and the output variable on the vertical axis.

The graph shows the number of hours, \(H\text{,}\) that the sun is above the horizon in Peoria, Illinois, on day \(t\text{,}\) where January 1 corresponds to \(t = 0\text{.}\)

  1. Which variable is the input, and which is the output?

  2. Approximately how many hours of sunlight are there in Peoria on day 150?

  3. On which days are there 12 hours of sunlight?

  4. What are the maximum and minimum values of \(H\text{,}\) and when do these values occur?

Peoria sunlight hours
Solution

  1. The input variable, \(t\text{,}\) appears on the horizontal axis. The number of daylight hours, \(H\text{,}\) is a function of the date. The output variable appears on the vertical axis.

  2. The point on the curve where \(t = 150\) has \(H \approx 14.1\text{,}\) so Peoria gets about 14.1 hours of daylight when \(t = 150\text{,}\) which is at the end of May.

  3. \(H = 12\) at the two points where \(t \approx 85\) (in late March) and \(t \approx 270\) (late September).

  4. The maximum value of 14.4 hours occurs on the longest day of the year, when \(t \approx 170\text{,}\) about three weeks into June. The minimum of 9.6 hours occurs on the shortest day, when \(t \approx 355\text{,}\) about three weeks into December.

The graph shows the elevation in feet, \(a\text{,}\) of the Los Angeles Marathon course at a distance \(d\) miles into the race. (Source: Los Angeles Times, March 3, 2005)

LA marathon elevation

  1. Which variable is the input, and which is the output?

  2. What is the elevation at mile 20?

  3. At what distances is the elevation 150 feet?

  4. What are the maximum and minimum values of \(a\text{,}\) and when do these values occur?

  5. The runners pass by the Los Angeles Coliseum at about 4.2 miles into the race. What is the elevation there?

Answer

  1. The input variable is \(d\text{,}\) and the output variable is \(a\text{.}\)

  2. Approximately \(210\) feet

  3. Approximately where \(d\approx 5\text{,}\) \(d\approx 11\text{,}\) \(d\approx 12\text{,}\) \(d\approx 16\text{,}\) \(d\approx 17.5\text{,}\) and \(d\approx 18\)

  4. The maximum value of \(300\) feet occurs at the start, when \(d = 0\text{.}\) The minimum of \(85\) feet occurs when \(d\approx 15\text{.}\)

  5. Approximately \(165\) feet

Subsection Functions Defined by Equations

Example 1.26 illustrates a function defined by an equation.

As of 2016, One World Trade Center in New York City is the nation’s tallest building, at 1776 feet. If an algebra book is dropped from the top of One World Trade Center, its height above the ground after \(t\) seconds is given by the equation

\begin{equation*} h = 1776 - 16t^2 \end{equation*}

Thus, after \(\alert{1}\) second the book’s height is

\begin{equation*} h = 1776 - 16(\alert{1})^2 = 1760 \text{ feet} \end{equation*}

After \(\alert{2}\) seconds its height is

\begin{equation*} h = 1776 - 16(\alert{2})^2 = 1712 \text{ feet} \end{equation*}

For this function, \(t\) is the input variable and \(h\) is the output variable. For any value of \(t\text{,}\) a unique value of \(h\) can be determined from the equation for \(h\text{.}\) We say that \(h\) is a function of \(t\text{.}\)

Write an equation that gives the volume, \(V\text{,}\) of a sphere as a function of its radius, \(r\text{.}\)

Answer

\(V = \dfrac{4}{3}\pi r^3\)

Subsection Function Notation

There is a convenient notation for discussing functions. First, we choose a letter, such as \(f\text{,}\) \(g\text{,}\) or \(h\) (or \(F\text{,}\) \(G\text{,}\) or \(H\)), to name a particular function. (We can use any letter, but these are the most common choices.)

For instance, in Example 1.26, the height, \(h\text{,}\) of a falling algebra book is a function of the elapsed time, \(t\text{.}\) We might call this function \(f\text{.}\) In other words, \(f\) is the name of the relationship between the variables \(h\) and \(t\text{.}\) We write

\begin{equation*} h = f (t) \end{equation*}

which means " \(h\) is a function of \(t\text{,}\) and \(f\) is the name of the function."

Caution 1.28.

The new symbol \(f(t)\text{,}\) read " \(f\) of \(t\text{,}\)" is another name for the height, \(h\text{.}\) The parentheses in the symbol \(f(t)\) do not indicate multiplication. (It would not make sense to multiply the name of a function by a variable.) Think of the symbol \(f(t)\) as a single variable that represents the output value of the function.

With this new notation we may write

\begin{equation*} h = f (t) = 1776 - 16t^2 \end{equation*}

or just

\begin{equation*} f (t) = 1776 - 16t^2 \end{equation*}

instead of

\begin{equation*} h = 1776 - 16t^2 \end{equation*}

to describe the function.

Note 1.29.

Perhaps it seems complicated to introduce a new symbol for \(h\text{,}\) but the notation \(f(t)\) is very useful for showing the correspondence between specific values of the variables \(h\) and \(t\text{.}\)

In Example 1.26, the height of an algebra book dropped from the top of One World Trade Center is given by the equation

\begin{equation*} h = 1776 - 16t^2 \end{equation*}

We see that

when \(t=1\) \(h=1760\)
when \(t=2\) \(h=1712\)

Using function notation, these relationships can be expressed more concisely as

\(f(1)=1760\) and \(f(2)=1712\)

which we read as " \(f\) of 1 equals 1760" and " \(f\) of 2 equals 1712." The values for the input variable, \(t\text{,}\) appear inside the parentheses, and the values for the output variable, \(h\text{,}\) appear on the other side of the equation.

Remember that when we write \(y = f(x)\text{,}\) the symbol \(f(x)\) is just another name for the output variable.

Function Notation.
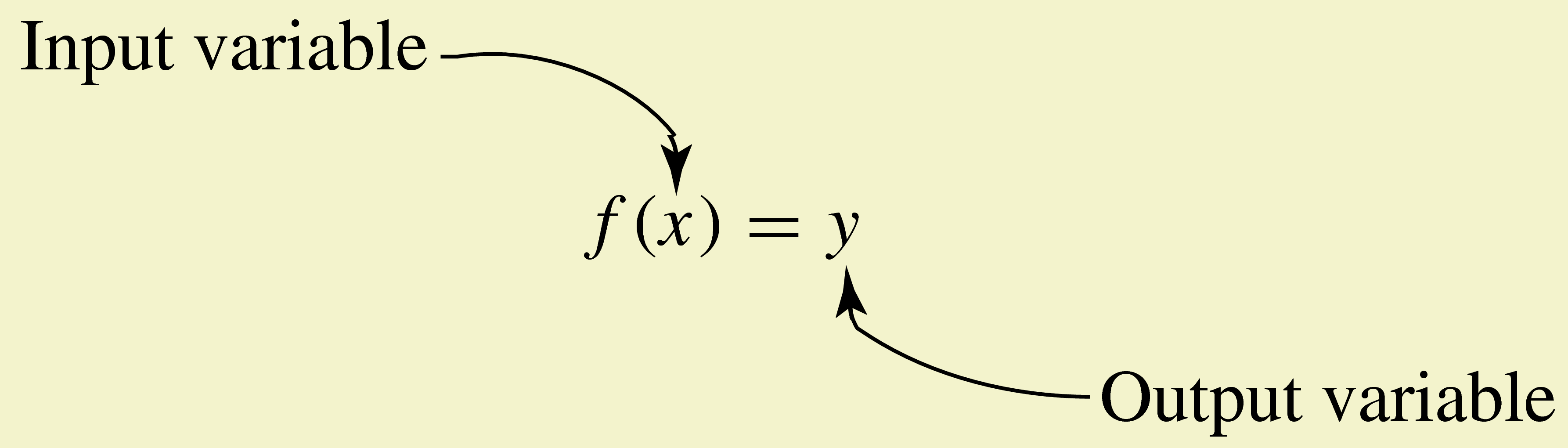
Function Notation

Let \(F\) be the name of the function defined by the graph in Example 1.24, the number of hours of daylight in Peoria.

  1. Use function notation to state that \(H\) is a function of \(t\text{.}\)

  2. What does the statement \(F(15) = 9.7\) mean in the context of the problem?

Answer

  1. \(H = F(t)\)

  2. The sun is above the horizon in Peoria for \(9.7\) hours on January 16.

Subsection Evaluating a Function

Finding the value of the output variable that corresponds to a particular value of the input variable is called evaluating the function.

Let \(g\) be the name of the postage function defined by the table in Example 1.20 b. Find \(g(1)\text{,}\) \(g(3)\text{,}\) and \(g(6.75\)).

Solution

According to the table,

when \(w=1\text{,}\) \(p=0.47\) so \(g(1)=0.47\)
when \(w=3\text{,}\) \(p=0.89\) so \(g(3)=0.89\)
when \(w=6.75\text{,}\) \(p=1.73\) so \(g(6.75)=1.73\)

Thus, a letter weighing 1 ounce costs $0.47 to mail, a letter weighing 3 ounces costs $0.89, and a letter weighing 6.75 ounces costs $1.73.

When you exercise, your heart rate should increase until it reaches your target heart rate. The table shows target heart rate, \(r = f(a)\text{,}\) as a function of age.

\(a\) \(20\) \(25\) \(30\) \(35\) \(40\) \(45\) \(50\) \(55\) \(60\) \(65\) \(70\)
\(r\) \(150\) \(146\) \(142\) \(139\) \(135\) \(131\) \(127\) \(124\) \(120\) \(116\) \(112\)

  1. Find \(f(25)\) and \(f(50)\text{.}\)

  2. Find a value of \(a\) for which \(f(a) = 135\text{.}\)

Answer

  1. \(f (25) = 146, ~~f (50) = 127\)

  2. \(a = 40\)

If a function is described by an equation, we simply substitute the given input value into the equation to find the corresponding output, or function value.

The function \(H\) is defined by \(H=f(s) = \dfrac{\sqrt{s+3}}{s}\text{.}\) Evaluate the function at the following values.

  1. \(s=6\)

  2. \(s=-1\)

Solution

  1. \(f(\alert{6})=\dfrac{\sqrt{\alert{6}+3}}{\alert{6}}= \dfrac{\sqrt{9}}{6}=\dfrac{3}{6}=\dfrac{1}{2}\text{.}\) Thus, \(f(6)=\dfrac{1}{2}\text{.}\)

  2. \(f(\alert{-1})=\dfrac{\sqrt{\alert{-1}+3}}{\alert{-1}}= \dfrac{\sqrt{2}}{-1}=-\sqrt{2}\text{.}\) Thus, \(f(-1)=-\sqrt{2}\text{.}\)

Complete the table displaying ordered pairs for the function \(f(x) = 5 - x^3\text{.}\) Evaluate the function to find the corresponding \(f(x)\)-value for each value of \(x\text{.}\)

\(x\) \(f(x)\)
\(-2\) \(\) \(f(\alert{-2})=5-(\alert{-2})^3=~\)
\(0\) \(\) \(f(\alert{0})=5-\alert{0}^3=\)
\(1\) \(\) \(f(\alert{1})=5-\alert{1}^3=\)
\(3\) \(\) \(f(\alert{3})=5-\alert{3}^3=\)
Answer
\(x\) \(f(x)\)
\(-2\) \(13 \)
\(0\) \(5\)
\(1\) \(4\)
\(3\) \(-22\)

To simplify the notation, we sometimes use the same letter for the output variable and for the name of the function. In the next example, \(C\) is used in this way.

TrailGear decides to market a line of backpacks. The cost, \(C\text{,}\) of manufacturing backpacks is a function of the number, \(x\text{,}\) of backpacks produced, given by the equation

\begin{equation*} C(x) = 3000 + 20x \end{equation*}

where \(C(x)\) is measured in dollars. Find the cost of producing 500 backpacks.

Solution

To find the value of \(C\) that corresponds to \(x = \alert{500}\text{,}\) evaluate \(C(500)\text{.}\)

\begin{equation*} C(\alert{500}) = 3000 + 20(\alert{500}) = 13,000 \end{equation*}

The cost of producing 500 backpacks is $13,000.

The volume of a sphere of radius \(r\) centimeters is given by

\begin{equation*} V = V(r) = \frac{4}{3}\pi r^3 \end{equation*}

Evaluate \(V(10)\) and explain what it means.

Answer

\(V(10) = 4000\pi/3\approx 4188.79 \text{ cm}^3\) is the volume of a sphere whose radius is \(10\) cm.

Subsection Operations with Function Notation

Sometimes we need to evaluate a function at an algebraic expression rather than at aspecific number.

TrailGear manufactures backpacks at a cost of

\begin{equation*} C(x) = 3000 + 20x \end{equation*}

for \(x\) backpacks. The company finds that the monthly demand for backpacks increases by 50% during the summer. The backpacks are produced at several small co-ops in different states.

  1. If each co-op usually produces \(b\) backpacks per month, how many should it produce during the summer months?
  2. What costs for producing backpacks should the company expect during the summer?
Solution
  1. An increase of 50% means an additional 50% of the current production level, \(b\text{.}\) Therefore, a co-op that produced \(b\) backpacks per month during the winter should increase production to \(b + 0.5b\text{,}\) or \(1.5b\) backpacks per month in the summer.
  2. The cost of producing \(1.5b\) backpacks will be
    \begin{equation*} C(\alert{1.5b}) = 3000 + 20(\alert{1.5b}) = 3000 + 30b \end{equation*}

A spherical balloon has a radius of 10 centimeters.

  1. If we increase the radius by \(h\) centimeters, what will the new volume be?
  2. If \(h = 2\text{,}\) how much did the volume increase?
Answer

  1. \(V(10 + h) = \dfrac{4}{3}\pi(10 + h)^3 \text{ cm}^3\)

  2. By \(3049.44 \text{ cm}^3\)

Evaluate the function \(f(x)=4x^2 - x + 5\) for the following expressions.

  1. \(\displaystyle x = 2h\)
  2. \(\displaystyle x = a + 3\)
Solution

  1.  

    \(\begin{aligned}[t] f(\alert{2h}) \amp= 4(\alert{2h})^2-(\alert{2h}) + 5\\ \amp= 4(4h^2)-2h+5\\ \amp= 16h^2 - 2h + 5\\ \end{aligned}\)

  2.  

    \(\begin{aligned}[t] f(\alert{a+3}) \amp= 4(\alert{a+3})^2-(\alert{a+3})+5\\ \amp= 4(a^2+6a+9)-a-3+5\\ \amp= 4a^2+24a+36 - a + 2\\ \amp= 4a^2+23a + 38\\ \end{aligned}\)

Caution 1.41.

In Example 1.40, notice that

\begin{equation*} f(2h) \ne 2 f(h) \end{equation*}

and

\begin{equation*} f(a + 3) \ne f(a) + f(3) \end{equation*}

To compute \(f(a) + f(3)\text{,}\) we must first compute \(f(a)\) and \(f(3)\text{,}\) then add them:

\begin{equation*} \begin{aligned}[t] f(a)+f(3)\amp= (4a^2-a+5)+(4\cdot 3^2-3+5) \\ \amp= 4a^2 - a + 43\\ \end{aligned} \end{equation*}

In general, it is not true that \(f(a + b) = f(a) + f(b)\text{.}\) Remember that the parentheses in the expression \(f(x)\) do not indicate multiplication, so the distributive law does not apply to the expression \(f(a + b)\text{.}\)

Let \(f(x) = x^3 - 1\) and evaluate each expression.

  1. \(\displaystyle f(2) + f(3)\)
  2. \(\displaystyle f(2 + 3)\)
  3. \(\displaystyle 2 f(x) + 3\)
Answer

  1. \(33\)

  2. \(124\)

  3. \(2x^3 + 1\)

Subsection Compostion and other Operations with Functions

(Note, some information found in this section has come from an OpenStax textbook titled "College Algebra". Access for free at this link.)

In Example 1.40 you were asked to evaluate the function \(f(x)=4x^2-x+5\) at \(x=2h\text{.}\) We can ask this question using composition notation. Let \(f(x)=4x^2-x+5\) and \(g(h)=2h\text{,}\) and find \((f\circ g)(h)\text{,}\) or, \(f(g(h))\text{.}\) The idea with composition is that you do not only evaluate a function at a point, but at another function. The end result is a new function.

The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. The resulting function is known as a composite function. We represent this combination by the following notation:

\begin{equation*} (f\circ g)(x)=f(g(x)). \end{equation*}

We read the left-hand side as " \(f\) composed with \(g\) at \(x\text{,}\)" and the right-hand side as " \(f\) of \(g\) of \(x\)". The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol \(\circ\) is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. However, it is important not to confuse function composition with multiplication, because in most cases \(f(g(x))\neq f(x)g(x)\text{.}\)

It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. In the equation above, the function \(g\) takes the input, \(x\text{,}\) first and yields an output, \(g(x)\text{.}\) Then the function \(f\) takes \(g(x)\) as an input and yields an output, \(f(g(x))\text{.}\)

Just like subtraction, order matters. Typically, \(f(g(x))\neq g(f(x))\text{,}\) so it is important to understand which is the "inner" function and which is the "outer" function.

Let \(f(x) = x^2-3x\) and \(g(x) = x+2\text{.}\)

  1. Find \(f(g(x))\text{.}\)

  2. Find \(g(f(x))\text{.}\)

Solution

  1. \(\begin{aligned}[t] f(g(x)) = \amp f(x+2)\\ = \amp (x+2)^2-3(x+2) \\ = \amp (x^2+4x+4)-(3x+6)\\ = \amp x^2+4x+4-3x-6\\ = \amp x^2 + x - 2 \end{aligned}\)

  2. \(\begin{aligned}[t] g(f(x)) = \amp g(x^2-3x)\\ = \amp (x^2-3x)+2\\ = \amp x^2-3x+2\\ \end{aligned} \)

Let \(f(x)=-2x^2+3x\) and \(g(x)=5x+9\text{.}\)

  1. Find \(f(g(x))\text{.}\)

  2. Find \(g(f(x))\text{.}\)

  3. Find \(g(g(x))\text{.}\)

Solution

  1. \(f(g(x))=-50x^2-165x-135\text{.}\)

  2. \(g(f(x)) = -10x^2+15x+9\text{.}\)

  3. \(g(g(x)) = 25x+54\text{.}\)

The same process holds true if you want to evalute a composition of functions at a given point.

Let \(f(x)=\sqrt{4+x}\) and \(g(x)=x+5\text{.}\)

  1. Find \(f(g(0))\text{.}\)

  2. Find \(g(f(0))\text{.}\)

  3. Find \(f(g(5))\text{.}\)

  4. Find \(g(f(5))\text{.}\)

Solution

  1. \(f(g(0))\text{.}\) Using the order of operations, we want to start inside and work our way out. \(g(0)=0+5=5\text{.}\) Now let us look at the original problem and replace \(g(0)\) with \(5\text{.}\) So we can evaluate \(f(g(0))=f(5)=\sqrt{4+5}=\sqrt{9}=3\text{.}\)

  2. \(g(f(0))\text{.}\) First, evaluate \(f(0)=\sqrt{4+0}=\sqrt{4}=2\text{.}\) Finally, \(g(f(0))=g(2)=2+5=7\text{.}\)

  3. Another way that you can write the solution, all at once, is as follows. \(f(g(5))=f(5+5)=f(10)=\sqrt{4+10}=\sqrt{14}\text{.}\) (Notice, we always want exact solutions unless stated otherwise. Often in applications problems it is sufficient to use rounded solutions.)

  4. \(g(f(5))=g(\sqrt{4+5})=g(\sqrt{9})=g(3)=3+5=8\text{.}\)

Let \(h(x)=\dfrac{2}{3}x+6\) and \(j(x)=x^2+2x\text{.}\)

  1. Find \(h(j(2))\text{.}\)

  2. Find \(j(h(2))\text{.}\)

  3. Find \(h(j(3))\text{.}\)

  4. Find \(j(j(1))\text{.}\)

Solution

  1. \(h(j(2)) = \dfrac{34}{3}\text{.}\)

  2. \(j(h(2)) = \dfrac{616}{9}\text{.}\)

  3. \(h(j(3)) = 16\text{.}\)

  4. \(j(j(1)) = 15\text{.}\)

Composition of functions has very useful applications, and more than likely you have done it yourself. This will appear in "day-to-day" life when you have to evaluate a function and use the output you just found to evaulate a different function.

Suppose there is a function, \(A(d)\text{,}\) which gives the pain level on a scale of \(0\) to \(10\) experienced by a patient with \(d\) milligrams of a pain-reducing drug in her system. There is another function \(m(t)\) which gives the number of milligrams of the drug in the patient's system after \(t\) minutes.

A nurse is asked how long it will be until her patient will be at pain level of \(3\text{.}\) Which of the 4 options below indicate how she would evaluate this?

  1. \(A(m(t))=3\)

  2. \(A(m(3))\)

  3. \(m(A(d))=3\)

  4. \(m(A(3))\)

Solution

Let us first look at what order you evaluate the functions: \(A(m(t))\) or \(m(A(d))\text{.}\) A nice way to determine order is to examine input and output variables. \(A(d)\) has the input of milligrams and output of pain scale. \(m(t)\) has the input of time and output of milligrams. This means we have to match up the output of \(m(t)\) with the input of \(A(d)\text{.}\) Right away, this means we want option (a) or (b), since the order of composition is right. Notice, if we are asked "how long", this means we want to solve for the variable \(t\text{.}\) The pain level is at \(3\text{,}\) which means \(A(d)=3\text{.}\) The only way both of these is satisfied is in option (a).

Composition of functions is not the only way that we can combine two functions: we can also add, subtract, multiply and divide. Note, mathematicians like to simplify as much as possible, and have created shorthand notation for various concepts. For instance: \(\begin{aligned}[t] (f+g)(x) = \amp f(x)+g(x),\\ (f-g)(x) = \amp f(x)-g(x),\\ (fg)(x) = \amp f(x)g(x),\\ \left(\dfrac{f}{g}\right)(x) = \amp \dfrac{f(x)}{g(x)}, \qquad \text{ provided } g(x)\neq 0.\\ \end{aligned}\)

Note that multiplication and composition are different function operations. Multiplication is the product of two functions. We notate multiplication of functions in the following ways: \((fg)(x)=f(x)g(x)=(f\cdot g)(x)=f(x)\cdot g(x)\text{.}\)

Let \(f(x) = -x^2+8x-15\) and \(g(x)=x^2-2x-15\text{.}\)

  1. Find \((f+g)(x)\text{.}\)

  2. Find \((f-g)(x)\text{.}\)

  3. Find \((fg)(x)\text{.}\)

  4. Find \(\left(\dfrac{f}{g}\right)(x)\text{.}\)

Solution

  1. \(\begin{aligned}[t] (f+g)(x) = \amp f(x)+g(x)\\ = \amp (-x^2+8x-15) + (x^2-2x-15)\\ = \amp -x^2+8x-15 + x^2-2x-15\\ = \amp 6x -30 \end{aligned}\)

  2. When subtracting functions be sure to subtract \emph{all} of the second function. Putting parentheses around the second function will help you remember to do this. \(\begin{aligned}[t] (f-g)(x) = \amp f(x)-g(x)\\ = \amp (-x^2+8x-15) - (x^2-2x-15)\\ = \amp -x^2+8x-15 -x^2+2x+15\\ = \amp -2x^2 +10x \end{aligned}\)

  3. \(\begin{aligned}[t] (fg)(x) = \amp f(x) g(x)\\ = \amp (-x^2+8x-15)(x^2-2x-15)\\ = \amp -x^4 + 2x^3+15x^2 +8x^3-16x^2-120x - 15x^2+30x+225 \\ = \amp - x^4 +10x^3 -16x^2-90x+225 \end{aligned}\)

  4. \(\begin{aligned}[t] \left(\dfrac{f}{g}\right)(x) = \amp \dfrac{-x^2+8x-15}{x^2-2x-15}\\ = \amp \dfrac{(-x+3)(x-5)}{(x-5)(x+3)}\\ = \amp \dfrac{-x+3}{x+3} \end{aligned}\)

Let \(f(x) = x^2+3x+2\) and \(g(x)=x^2+6x+8\text{.}\)

  1. Find \((f+f)(x)\text{.}\)

  2. Find \((g-f)(x)\text{.}\)

  3. Find \((fg)(x)\text{.}\)

  4. Find \(\left(\dfrac{f}{g}\right)(x)\text{.}\)

Solution

  1. \((f+f)(x) = 2x^2+6x+4\)

  2. \((g-f)(x) = 3x+6\)

  3. \((fg)(x) = x^4+9x^3+28x^2+36x+16\)

  4. \(\left(\dfrac{f}{g}\right)(x) = \dfrac{x+1}{x+4}\)

Subsection Section Summary

Subsubsection Vocabulary

Look up the definitions of new terms in the Glossary.

  • Function
  • Input variable
  • Independent variable
  • Function value
  • Dependent variable
  • Output variable

Subsubsection CONCEPTS

  1. A function is a rule that assigns to each value of the input variable a unique value of the output variable.

  2. Functions may be defined by words, tables, graphs, or equations.

  3. Function notation: \(y = f (x)\text{,}\) where \(x\) is the input and \(y\) is the output.

Subsubsection STUDY QUESTIONS

  1. What property makes a relation between two variables a function?

  2. Name three ways to define a function.

  3. Give an example of a function in which two distinct values of the input variable correspond to the same value of the output variable.

  4. Use function notation to write the statement "\(G\) defines \(w\) as a function of \(p\text{.}\)"

  5. Give an example of a function for which \(f (2 + 3)\ne f (2) + f (3)\text{.}\)

Subsubsection SKILLS

Practice each skill in the Homework  problems listed.

  1. Decide whether a relationship between two variables is a function: #1–26

  2. Evaluate a function defined by a table, a graph, or an equation: #27–54

  3. Choose appropriate scales for the axes: #5–12

  4. Interpret function notation: #31–34, 49–54

  5. Simplify expressions involving function notation: #59–76

Exercises Homework 1.2

For which of Problems 1-6 is the second quantity a function of the first? Explain your answers.

1.

Price of an item; sales tax on the item at 4%

2.

Time traveled at constant speed; distance traveled

3.

Number of years of education; annual income

4.

Distance flown in an airplane; price of the ticket

5.

Volume of a container of water; the weight of the water

6.

Amount of a paycheck; amount of Social Security tax withheld

Each of the objects in Problems 7-14 establishes a correspondence between two variables. Suggest appropriate input and output variables and decide whether the relationship is a function.

7.

An itemized grocery receipt

8.

An inventory list

9.

An index

10.

A will

11.

An instructor's grade book

12.

An address book

13.

A bathroom scale

14.

A radio dial

Which of the tables in Problems 15-26 define the second variable as a function of the first variable? Explain why or why not.

15.
\(x\) \(t\)
\(-1\) \(2\)
\(0\) \(9\)
\(1\) \(-2\)
\(0\) \(-3\)
\(-1\) \(5\)
16.
\(y\) \(w\)
\(0\) \(8\)
\(1\) \(12\)
\(3\) \(7\)
\(5\) \(-3\)
\(7\) \(4\)
17.
\(x\) \(y\)
\(-3\) \(8\)
\(-2\) \(3\)
\(-1\) \(0\)
\(0\) \(-1\)
\(1\) \(0\)
\(2\) \(3\)
\(3\) \(8\)
18.
\(s\) \(t\)
\(2\) \(5\)
\(4\) \(10\)
\(6\) \(15\)
\(8\) \(20\)
\(6\) \(25\)
\(4\) \(30\)
\(2\) \(35\)
19.
\(r\) \(-4\) \(-2\) \(0\) \(2\) \(4\)
\(v\) \(6\) \(6\) \(3\) \(6\) \(8\)
20.
\(p\) \(-5\) \(-4\) \(-3\) \(-2\) \(-1\)
\(d\) \(-5\) \(-4\) \(-3\) \(-2\) \(-1\)
21.
Pressure (\(p\)) Volume (\(v\))
\(15\) \(100.0\)
\(20\) \(75.0\)
\(25\) \(60.0\)
\(30\) \(50.0\)
\(35\) \(42.8\)
\(40\) \(37.5\)
\(45\) \(33.3\)
\(50\) \(30.0\)
22.
Frequency (\(f\)) Wavelength (\(w\))
\(5\) \(60.0\)
\(10\) \(30.0\)
\(20\) \(15.0\)
\(30\) \(10.0\)
\(40\) \(7.5\)
\(50\) \(6.0\)
\(60\) \(5.0\)
\(70\) \(4.3\)
23.
Temperature (\(T\)) Humidity (\(h\))
Jan. 1 \(\hphantom{000}34\degree\)F \(42\%\)
Jan. 2 \(\hphantom{000}36\degree\)F \(44\%\)
Jan. 3 \(\hphantom{000}35\degree\)F \(47\%\)
Jan. 4 \(\hphantom{000}29\degree\)F \(50\%\)
Jan. 5 \(\hphantom{000}31\degree\)F \(52\%\)
Jan. 6 \(\hphantom{000}35\degree\)F \(51\%\)
Jan. 7 \(\hphantom{000}34\degree\)F \(49\%\)
24.
Inflation
rate (\(I\))		 Unemployment
rate (\(U\))
1972 \(\hphantom{000}5.6\%\) \(5.1\%\)
1973 \(\hphantom{000}6.2\%\) \(4.5\%\)
1974 \(\hphantom{000}10.1\%\) \(4.9\%\)
1975 \(\hphantom{000}9.2\%\) \(7.4\%\)
1976 \(\hphantom{000}5.8\%\) \(6.7\%\)
1977 \(\hphantom{000}5.6\%\) \(6.8\%\)
1978 \(\hphantom{000}6.7\%\) \(7.4\%\)
25.
Adjusted gross
income (\(I\))		 Tax bracket (\(T\))
$\(0-2479\) \(0\%\)
$\(2480-3669\) \(4.5\%\)
$\(3670-4749\) \(12\%\)
$\(4750-7009\) \(14\%\)
$\(7010-9169\) \(15\%\)
$\(9170-11,649\) \(16\%\)
$\(11,650-13,919\) \(18\%\)
26.
Cost of
merchandise (\(M\))		 Shipping
charge (\(C\))
\(\$0.01-10.00\) \(\$2.50\)
\(10.01-20.00\) \(3.75\)
\(20.01-35.00\) \(4.85\)
\(35.01-50.00\) \(5.95\)
\(50.01-75.00\) \(6.95\)
\(75.01-100.00\) \(7.95\)
Over \(100.00\) \(8.95\)
27.

The function described in Problem 21 is called \(g\text{,}\) so that \(v = g( p)\text{.}\) Find the following:

  1. \(g(25)\)

  2. \(g(40)\)

  3. \(x\) so that \(g(x) = 50\)

28.

The function described in Problem 22 is called \(h\text{,}\) so that \(w = h( f)\text{.}\) Find the following:

  1. \(h(20)\)

  2. \(h(60)\)

  3. \(x\) so that \(h(x) = 10\)

29.

The function described in Problem 25 is called \(T\text{,}\) so that \(T = T( I)\text{.}\) Find the following:

  1. \(T(8750)\)

  2. \(T(6249)\)

  3. \(x\) so that \(T(x) = 15\%\)

30.

The function described in Problem 26 is called \(C\text{,}\) so that \(C = C( M)\text{.}\) Find the following:

  1. \(C(11.50)\)

  2. \(C(47.24)\)

  3. \(x\) so that \(C(x) = 7.95\)

31.

Data indicate that U.S. women are delaying having children longer than their counterparts 50 years ago. The table shows \(f(t)\) the percent of 20–24-year-old women in year \(t\) who had not yet had children. (Source: U.S. Dept of Health and Human Services)

Year (\(t\)) \(1960\) \(1965\) \(1970\) \(1975\) \(1980\) \(1985\) \(1990\) \(1995\) \(2000\)
Percent of
women		 \(47.5\) \(51.4\) \(47.0\) \(62.5\) \(66.2\) \(67.7\) \(68.3\) \(65.5\) \(66.0\)

  1. Evaluate \(f (1985)\) and explain what it means.

  2. Estimate a solution to the equation \(f (t) = 68\) and explain what it means.

  3. In 1997, \(64.9\%\) of 20–24-year-old women had not yet had children. Write an equation with function notation that states this fact.

32.

The table shows \(f (t)\text{,}\) the death rate (per 100,000 people) from HIV among 15–24-year-olds, and \(g(t)\text{,}\) the death rate from HIV among 25–34-year-olds, for selected years from 1997 to 2002. (Source: U.S. Dept of Health and Human Services)

Year \(1987\) \(1988\) \(1989\) \(1990\) \(1992\) \(1994\) \(1996\) \(1998\) \(2000\) \(2002\)
15–24-year-olds \(1.3\) \(1.4\) \(1.6\) \(1.5\) \(1.6\) \(1.8\) \(1.1\) \(0.6\) \(0.5\) \(0.4\)
25–34-year-olds \(11.7\) \(14.0\) \(17.9\) \(19.7\) \(24.2\) \(28.6\) \(19.2\) \(8.1\) \(6.1\) \(4.6\)

  1. Evaluate \(f (1995)\) and explain what it means.

  2. Find a solution to the equation \(g (t) = 28.6\) and explain what it means.

  3. In 1988, the death rate from HIV for 25–34-year-olds was \(10\) times the corresponding rate for 15–24-year-olds. Write an equation with function notation that states this fact.

33.

When you exercise, your heart rate should increase until it reaches your target heart rate. The table shows target heart rate, \(r = f (a)\text{,}\) as a function of age.

\(a\) \(20\) \(25\) \(30\) \(35\) \(40\) \(45\) \(50\) \(55\) \(60\) \(65\) \(70\)
\(r\) \(150\) \(146\) \(142\) \(139\) \(135\) \(131\) \(127\) \(124\) \(120\) \(116\) \(112\)

  1. Does \(f (50) = 2 f (25)\text{?}\)

  2. Find a value of a for which \(f (a) = 2a\text{.}\) Is \(f (a) = 2a\) for all values of \(a\text{?}\)

  3. Is \(r = f (a)\) an increasing function or a decreasing function?

34.

The table shows \(M = f (d)\text{,}\) the men's Olympic record time, and \(W = g(d)\text{,}\) the women's Olympic record time, as a function of the length, \(d\text{,}\) of the race. For example, the women’s record in the 100 meters is 10.62 seconds, and the men’s record in the 800 meters is 1 minute, 42.58 seconds. (Source: www.hickoksports.com)

Distance
(meters)		 \(100\) \(200\) \(400\) \(800\) \(1500\) \(5000\) \(10,000\)
Men \(9.63\) \(19.30\) \(43.03\) \(1:40.91\) \(3:32.07\) \(12:57.82\) \(27:01.17\)
Women \(10.62\) \(21.34\) \(48.25\) \(1:53.43\) \(3:53.96\) \(14:26.17\) \(29:17.45\)

  1. Does \(f (800) = 2 f (400)\text{?}\) Does \(g(400) = 2g(200)\text{?}\)

  2. Find a value of \(d\) for which \(f (2d)\lt 2f (d)\text{.}\) Is there a value of \(d\) for which \(g(2d)\lt 2g(d)\text{?}\)

In Problems 35—40, use the graph of the function to answer the questions.

35.

The graph shows \(C\) as a function of \(t\text{.}\) \(C\) stands for the number of students (in thousands) at State University who consider themselves computer literate, and \(t\) represents time, measured in years since 1990.

increasing concave up graph

  1. When did \(2000\) students consider themselves computer literate?

  2. How long did it take that number to double?

  3. How long did it take for the number to double again?

  4. How many students became computer literate between January 1992 and June 1993?

36.

The graph shows \(P\) as a function of \(t\text{.}\) \(P\) is the number of people in Cedar Grove who owned a portable DVD player \(t\) years after 2000.

increasing concave down graph

  1. When did 3500 people own portable DVD players?

  2. How many people owned portable DVD players in 2005?

  3. The number of owners of portable DVD players in Cedar Grove seems to be leveling off at what number?

  4. How many people acquired portable DVD players between 2001 and 2004?

37.

The graph shows the revenue, \(R\text{,}\) a movie theater collects as a function of the price, \(d\text{,}\) it charges for a ticket.

concave down graph

  1. What is the revenue if the theater charges $\(12.00\) for a ticket?

  2. What should the theater charge for a ticket in order to collect $\(1500\) in revenue?

  3. For what values of \(d\) is \(R\gt 1875\text{?}\)

38.

The graph shows \(S\) as a function of \(w\text{.}\) \(S\) represents the weekly sales of a best-selling book, in thousands of dollars, \(w\) weeks after it is released.

bell-shaped graph

  1. In which weeks were sales over $\(7000\text{?}\)

  2. In which week did sales fall below $\(5000\) on their way down?

  3. For what values of \(w\) is \(S\gt 3.4\text{?}\)

39.

The graph shows the federal minimum wage, \(M\text{,}\) as a function of time, \(t\text{,}\) adjusted for inflation to reflect its buying power in 2004 dollars. (Source: www.infoplease.com)

unemployment rate

  1. When did the minimum wage reach its highest buying power, and what was it worth in 2004 dollars?

  2. When did the minimum wage fall to its lowest buying power after its peak, and what was its worth at that time?

  3. Give two years in which the minimum wage was worth $\(8\) in 2004 dollars.

40.

The graph shows the U.S. unemployment rate, \(U\text{,}\) as a function of time, \(t\text{,}\) for the years 1985–2004. (Source: U.S. Bureau of Labor Statistics)

unemployment rate

  1. When did the unemployment rate reach its highest value, and what was its highest value?

  2. When did the unemployment rate fall to its lowest value, and what was its lowest value?

  3. Give two years in which the unemployment rate was \(4.5\%\text{.}\)

In Problems 41–48, evaluate each function for the given values, if possible. If not, state why.

41.

\(f (x) = 6 - 2x\)

  1. \(f(3)\)

  2. \(f(-2)\)

  3. \(f(12.7)\)

  4. \(f\left(\dfrac{2}{3}\right)\)

42.

\(g(t) = 5t - 3\)

  1. \(g(1)\)

  2. \(g(-4)\)

  3. \(g(14.1)\)

  4. \(g\left(\dfrac{3}{4}\right)\)

43.

\(h(v) = 2v^2 - 3v + 1\)

  1. \(h(0)\)

  2. \(h(-1)\)

  3. \(h\left(\dfrac{1}{4}\right)\)

  4. \(h(-6.2)\)

44.

\(r (s) = 2s - s^2\)

  1. \(r(2)\)

  2. \(r(-4)\)

  3. \(r\left(\dfrac{1}{3}\right)\)

  4. \(r(-1.3)\)

45.

\(H(z) = \dfrac{2z - 3}{z + 2}\)

  1. \(H(4)\)

  2. \(H(-3)\)

  3. \(H\left(\dfrac{4}{3}\right)\)

  4. \(H(4.5)\)

46.

\(F(x) = \dfrac{1-x}{2x-3}\)

  1. \(F(0)\)

  2. \(F(-3)\)

  3. \(F\left(\dfrac{5}{2}\right)\)

  4. \(F(\dfrac{3}{2})\)

47.

\(E(t) =\sqrt{t-4}\)

  1. \(E(16)\)

  2. \(E(4)\)

  3. \(E(7)\)

  4. \(E(4.2)\)

48.

\(D(r) =\sqrt{5-r}\)

  1. \(D(4)\)

  2. \(D(-3)\)

  3. \(D(9)\)

  4. \(D(4.6)\)

49.

A sport utility vehicle costs $\(28,000\) and depreciates according to the formula

\begin{equation*} V(t) = 28,000 (1 - 0.08t) \end{equation*}

where \(V\) is the value of the vehicle after \(t\) years.

  1. Evaluate \(V(12)\) and explain what it means.

  2. Solve the equation \(V(t) = 0\) and explain what it means.

  3. If this year is \(t = n\text{,}\) what does \(V(n + 2)\) mean?

50.

In a profit-sharing plan, an employee receives a salary of

\begin{equation*} S(x) = 20,000 + 0.01x \end{equation*}

where \(x\) represents the company's profit for the year.

  1. Evaluate \(S(850,000)\) and explain what it means.

  2. Solve the equation \(S(x) = 30,000\) and explain what it means.

  3. If the company made a profit of \(p\) dollars this year, what does \(S(2p)\) mean?

51.

The number of compact cars that a large dealership can sell at price \(p\) is given by

\begin{equation*} N( p) = \dfrac{12,000,000}{p} \end{equation*}

  1. Evaluate \(N(6000)\) and explain what it means.

  2. As \(p\) increases, does \(N(p)\) increase or decrease? Why is this reasonable?

  3. If the current price for a compact car is \(D\text{,}\) what does \(2N(D)\) mean?

52.

A department store finds that the market value of its Christmas-related merchandise is given by

\begin{equation*} M(t) = \dfrac{600,000}{t},~~ t\le 30 \end{equation*}

where \(t\) is the number of weeks after Christmas.

  1. Evaluate \(M(2)\) and explain what it means.

  2. As \(t\) increases, does \(M(t)\) increase or decrease? Why is this reasonable?

  3. If this week \(t = n\text{,}\) what does \(M(n + 1)\) mean?

53.

The velocity of a car that brakes suddenly can be determined from the length of its skid marks, \(d\text{,}\) by

\begin{equation*} v(d) = \sqrt{12d} \end{equation*}

where \(d\) is in feet and \(v\) is in miles per hour.

  1. Evaluate \(v(250)\) and explain what it means.

  2. Estimate the length of the skid marks left by a car traveling at \(100\) miles per hour.

  3. Write your answer to part (b) with function notation.

54.

The distance, \(d\text{,}\) in miles that a person can see on a clear day from a height, \(h\text{,}\) in feet is given by

\begin{equation*} d(h) = 1.22\sqrt{h} \end{equation*}

  1. Evaluate \(d(20,320)\) and explain what it means.

  2. Estimate the height you need in order to see \(100\) miles.

  3. Write your answer to part (b) with function notation.

55.

The figure gives data about snowfall, air temperature, and number of avalanches on the Mikka glacier in Sarek, Lapland, in 1957. (Source: Leopold, Wolman, Miller, 1992)

three graphs

  1. During June and July, avalanches occurred over three separate time intervals. What were they?

  2. Over what three time intervals did snow fall?

  3. When was the temperature above freezing (\(0\degree\)C)?

  4. Using your answers to parts (a)–(c), make a conjecture about the conditions that encourage avalanches.

56.

The bar graph shows the percent of Earth's surface that lies at various altitudes or depths below the surface of the oceans. (Depths are given as negative altitudes.) (Source: Open University)

bar graph

  1. Read the graph and complete the table.

    Altitude (km) Percent of
    Earth's surface
    \(-7\) to \(-6\) \(\)
    \(-6\) to \(-5\) \(\)
    \(-5\) to \(-4\) \(\)
    \(-4\) to \(-3\) \(\)
    \(-3\) to \(-2\) \(\)
    \(-2\) to \(-1\) \(\)
    \(-1\) to \(0\) \(\)
    \(0\) to \(1\) \(\)
    \(1\) to \(2\) \(\)
    \(2\) to \(3\) \(\)
    \(3\) to \(4\) \(\)
    \(4\) to \(5\) \(\)

  2. What is the most common altitude? What is the second most common altitude??

  3. Approximately what percent of the Earth's surface is below sea level?

  4. The height of Mt. Everest is \(8.85\) kilometers. Can you think of a reason why it is not included in the graph?

57.

The graph shows the temperature of the ocean at various depths. (Source: Open University)

temperature vs depth

  1. Is depth a function of temperature?

  2. Is temperature a function of depth?

  3. The axes are scaled in an unusual way. Why is it useful to present the graph in this way?

58.

The graph shows the relationship between annual precipitation, \(p\text{,}\) in a region and the amount of erosion, measured in tons per square mile, \(s\text{.}\) (Source: Leopold, Wolman, Miller, 1992)

precipitation vs sediment yield

  1. Is the amount of erosion a function of the amount of precipitation?

  2. At what annual precipitation is erosion at a maximum, and what is that maximum?

  3. Over what interval of annual precipitation does erosion decrease?

  4. An increase in vegetation inhibits erosion, and precipitation encourages vegetation. What happens to the amount of erosion as precipitation increases in each of these three environments?

    desert shrub: \(0\lt p\lt 12\)
    grassland: \(12\lt p\lt 30\)
    forest: \(30\lt p\lt 60\)

In Problems 59—64, evaluate the function and simplify.

59.

\(G(s) = 3s^2 - 6s\)

  1. \(G(3a)\)

  2. \(G(a + 2)\)

  3. \(G(a) + 2\)

  4. \(G(-a)\)

60.

\(h(x) = 2x^2 + 6x - 3\)

  1. \(h(2a)\)

  2. \(h(a + 3)\)

  3. \(h(a) + 3\)

  4. \(h(-a)\)

61.

\(g(x) = 8\)

  1. \(g(2)\)

  2. \(g(8)\)

  3. \(g(a + 1)\)

  4. \(g(-x)\)

62.

\(f (t) = -3\)

  1. \(f (4)\)

  2. \(f (-3)\)

  3. \(f (b - 2)\)

  4. \(f (-t)\)

63.

\(P(x) = x^3 - 1\)

  1. \(P(2x)\)

  2. \(2P(x)\)

  3. \(P(x^2)\)

  4. \([P(x)]^2\)

64.

\(Q(t) = 5t^3\)

  1. \(Q(2t)\)

  2. \(2Q(t)\)

  3. \(Q(t^2)\)

  4. \([Q(t)]^2\)

In Problems 65—68, evaluate the function for the given expressions and simplify.

65.

\(f (x) = x^3\)

  1. \(f (a^2)\)

  2. \(a^3 \cdot f (a^3)\)

  3. \(f (ab)\)

  4. \(f (a + b)\)

66.

\(g(x) = x^4\)

  1. \(g(a^3)\)

  2. \(a^4\cdot g(a^4)\)

  3. \(g(ab)\)

  4. \(g(a + b)\)

67.

\(F(x) = 3x^5\)

  1. \(F(2a)\)

  2. \(2 F(a)\)

  3. \(F(a^2)\)

  4. \([F(a)]^2\)

68.

\(G(x) = 4x^3\)

  1. \(G(3a)\)

  2. \(3G(a)\)

  3. \(G(a^4)\)

  4. \([G(a)]^4\)

For the functions in Problems 69–76, compute the following:

  1. \(f (2) + f (3)\)

  2. \(f (2 + 3)\)

  3. \(f (a) + f (b)\)

  4. \(f (a + b)\)

For which functions does \(f (a + b) = f (a) + f (b)\) for all values of \(a\) and \(b\text{?}\)

69.

\(f (x) = 3x - 2\)

70.

\(f (x) = 1 - 4x\)

71.

\(f (x) = x^2 + 3\)

72.

\(f (x) = x^2 - 1\)

73.

\(f (x) =\sqrt{x+1} \)

74.

\(f (x) = \sqrt{6-x}\)

75.

\(f (x) =\dfrac{-2}{x} \)

76.

\(f (x) = \dfrac{3}{x}\)

77.

Use a table of values to estimate a solution to

\begin{equation*} f (x) = 800 + 6x - 0.2x^2 = 500 \end{equation*}

as follows:

  1. Make a table starting at \(x = 0\) and increasing by \(\Delta x = 10\text{,}\) as shown in the accompanying tables. Find two \(x\)-values \(a\) and \(b\) so that \(f (a)\gt 500\gt f (b)\text{.}\)

    \(x\) \(0\) \(10\) \(20\) \(30\) \(40\) \(50\) \(60\) \(70\) \(80\) \(90\) \(100\)
    \(f(x)\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\)

  2. Make a new table starting at \(x = a\) and increasing by \(\Delta x = 1\text{.}\) Find two \(x\)-values, \(c\) and \(d\text{,}\) so that \(f (c)\gt 500\gt f (d)\text{.}\)

  3. Make a new table starting at \(x = c\) and increasing by \(\Delta x = 0.1\text{.}\) Find two \(x\)-values, \(p\) and \(q\text{,}\) so that \(f (p)\gt 500\gt f (q)\text{.}\)

  4. Take the average of \(p\) and \(q\text{,}\) that is, set \(s = \dfrac{p + q}{2}\text{.}\) Then \(s\) is an approximate solution that is off by at most \(0.05\text{.}\)

  5. Evaluate \(f (s)\) to check that the output is approximately \(500\text{.}\)

78.

Use a table of values to estimate a solution to

\begin{equation*} f (x) = x^3 - 4x^2 + 5x = 18, 000 \end{equation*}

as follows:

  1. Make a table starting at \(x = 0\) and increasing by \(\Delta x = 10\text{,}\) as shown in the accompanying tables. Find two \(x\)-values \(a\) and \(b\) so that \(f (a)\lt 18,000\lt f (b)\text{.}\)

    \(x\) \(0\) \(10\) \(20\) \(30\) \(40\) \(50\) \(60\) \(70\) \(80\) \(90\) \(100\)
    \(f(x)\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\) \(\)

  2. Make a new table starting at \(x = a\) and increasing by \(\Delta x = 1\text{.}\) Find two \(x\)-values, \(c\) and \(d\text{,}\) so that \(f (c)\lt 18,000\lt f (d)\text{.}\)

  3. Make a new table starting at \(x = c\) and increasing by \(\Delta x = 0.1\text{.}\) Find two \(x\)-values, \(p\) and \(q\text{,}\) so that \(f (p)\lt 18,000\lt f (q)\text{.}\)

  4. Take the average of \(p\) and \(q\text{,}\) that is, set \(s = \dfrac{p + q}{2}\text{.}\) Then \(s\) is an approximate solution that is off by at most \(0.05\text{.}\)

  5. Evaluate \(f (s)\) to check that the output is approximately \(18,000\text{.}\)

79.

Use tables of values to estimate the positive solution to

\begin{equation*} f (x) = x^2 - \dfrac{1}{x} = 9000\text{,} \end{equation*}

accurate to within \(0.05\text{.}\)

80.

Use tables of values to estimate the positive solution to

\begin{equation*} f (x) = \dfrac{8}{x}+500-\dfrac{x^2}{9} = 300\text{,} \end{equation*}

accurate to within \(0.05\text{.}\)

81.

Let \(f(x)=-5x-5\) and \(g(x)=2x^2+1\text{.}\) Evaluate each of the following.

  1. \(g(f(4))\)

  2. \(f(g(-4))\)

  3. \(f(f(2))\)

  4. \(g(g(4))\)

  5. \((g-f)(2)\)

  6. \((fg)(-4)\)

82.

Answer "True" or "False": \(f(g(x))\) must always equal \(g(f(x))\text{.}\)

83.

Suppose \(f(x)=3x+1\) and \(g(x)= |x|\text{.}\) Evaluate each of the following.

  1. \(f(x)+g(x)\)

  2. \(g(x)-f(x)\)

  3. \(f(x)g(x)\)

  4. \(f(x)/g(x)\)

  5. \(f(g(x))\)

  6. \(g(f(x))\)

84.

Let \(f(x)=x^2-2\) and \(g(x)=\sqrt{x}+6\text{.}\) Find \(f(g(x))\) and \(g(f(x))\text{.}\)

  1. \(f(g(x))\)

  2. \(g(f(x))\)